Признаки делимости чисел:
Число делится на 2, если на 2 делится его последняя цифра.
Число делится на 3, если на 3 делится сумма его цифр.
Число делится на 4, если на 4 делится число, составленное из последних двух цифр.
Число делится на 5, если на 5 делится его последняя цифра.
Число делится на 6, если на 2 делится его последняя цифра, и делится на 3 сумма цифр (т.е. комбинация признаков на 2 и 3).
Число делится на 8, если на 8 делится число, составленное из последних трех цифр.
Число делится на 9, если на 9 делится сумма его цифр.
Число делится на 10, если последняя цифра числа – 0.
Число делится на 72, если на 8 делится число, составленное из последних трех цифр, и делится на 9 сумма цифр (т.е. комбинация признаков на 8 и 9, т.к. 72=8*9).
НОД (a;b) = НОД (a;a + b)
НОД (a;b) = НОД (a;a − b)
Если целые числа a и b взаимно просты, то их сумма a + b и произведение ab также являются взаимно простыми числами.
Если целые числа a и b являются взаимно простыми, то НОД (a + b;a − b) равен 1 или 2.
математики перешли на новый уровень
|
#151 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 6
4102 дня назад
|
+2
|
||
|
#152 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 10
4098 дней назад
|
+2
Здравствуйте! Я хочу рассказать о признаке делимости на 11!
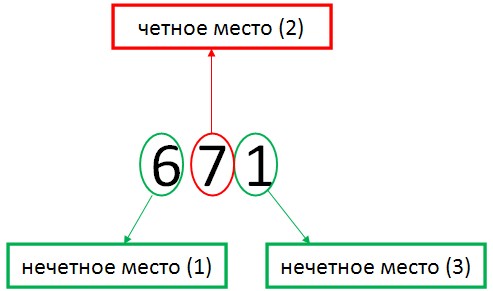
Существует и другие признаки делимости кроме перечисленных, но они на порядок сложнее. Для тех, кому интересно, приводим пример признака делимости на 11. Признак делимости на 11 +++++++++++++++++++++++++++++запомните!++++++++++++++++++++++++++++++++++++++ Число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11. ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ В самом деле признак делимости на 11 очень интересен, попробуем разобраться на примере: Проверим, делится ли 671 на 11 . Признак делимости на 11 Итак, цифры которые стоят на нечетных местах - это 6 (стоит на первом месте) и 1 (стоит на третьим месте). Цифра, которая стоит на четном месте это 7 (стоит на втором месте). 6 + 1 = 7. Сумма цифр стоящих на нечетном месте равна сумме цифр на четном месте, значит 671 делится на 11. Проверим делится ли 3905 на 11 . Цифры которые стоят на нечетных местах - это 3 (стоит на первом месте) и 0 (стоит на третьим месте). Цифры, которые стоят на четном месте это 9 (стоит на втором месте) и 5 (стоит на четвертом месте). 3 + 0 ≠ 9 + 5 → 3 ≠ 14 Сумма цифр, стоящих на нечетном месте, не равна сумме цифр на четном месте, но суммы цифр отличаются ровно на 11. 14 - 3 = 11. Значит 3905 делится на 11. Прикрепленные файлы:
Редактировалось: 1 раз (Последний: 8 октября 2014 в 19:37)
|
||
|
#153 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 38
г.Комсомольск-на-Амуре
4073 дня назад
|
+5
Моя задачка на делимость:
Коля и Вася живут в одном доме, на каждой лестничной клетке которого 4 квартиры. Коля живет на пятом этаже, в квартире 83, а Вася - на 3-ем этаже в квартире 169. Сколько этажей в доме ? Ответ :Если вести сквозной отсчет этажей, начиная с первого подъезда, то Коля живет на 21 этаже [83 : 4] = 20 (3). В своем подъезде Коля живет на 5 этаже, поэтому в подъездах, предшествующих Колиному, 16 этажей. 16 делится лишь на числа, кратные 2 поэтому в доме может быть либо 16 этажей, либо 8 этажей (вариант четырехэтажного дома исключаем, поскольку Коля живет на 5 этаже). Вася живет на 43 этаже, считая от первого этажа первого подъезда [169 : 4] = 42 (1). Значит в подъездах, предшествующих Васиному, 40 этажей. 40 делится на 8, но не делится на 16, следовательно, в доме 8 этажей. Замечание. В процессе решения задачи мы определили числа этажей (16 и 40) в двух разных группах подъездов. Число этажей в каждой группе подъездов кратно числу этажей в доме, оно равно произведению числа этажей в доме на число подъездов в группе. Задача сводится к нахождению общего делителя чисел 16 и 40 ( с уcловием, что делитель этот не меньше 5-ти). Редактировалось: 2 раза (Последний: 8 октября 2014 в 17:55)
|
||
|
#154 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 12
Оффлайн
|
+2
Признаки делимости на 10, на 5.
Натуральное число делится на 10 без остатка только в том случае, если оно оканчивается на нуль. Если последняя цифра натурального числа не 0, то число на 10 без остатка не делится. Числа 10, 20, 30 … , 220, 1200, 1210 … и т. д. делятся на 10 без остатка. Например: 20 : 10 = 2; 220 : 10 = 22; 2330 : 10 = 233. Натуральное число делится на 5 без остатка в том случае, если оно оканчивается на 0 или на 5. Числа 5, 10, 15, 20 … , 220, 225, … и т. д. делятся на 5 без остатка. Например: 20 : 5 = 4; 225 : 5 = 45; 2335 : 5 = 467 . Если последняя цифра натурального числа не 0 и не 5, то число на 5 без остатка не делится. Например: 23 : 5 = 4 целых 3/5; 221 : 5 = 44 целых 1/5; 2334 : 5 = 466 целых 4/5. Редактировалось: 5 раз (Последний: 8 октября 2014 в 19:28)
|
||
|
#155 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 174
г.Комсомольск-на-Амуре
3929 дней назад
|
+3
Какие хорошие последние свойства, Костя! Сумеешь на примерах их пояснить?Добавлено спустя 2 минутыМолодец, Никита. Ятебе тоже слово на уроке предоставлю,хорошо?
Никита Киселёв: Добавлено спустя 5 минутМолодец, Яночка. Очень хорошиий пример привела уравнения,решаемого с помощью признаков делимости.Здравствуйте! Я хочу рассказать о признаке делимости на 11! Существует и другие признаки делимости кроме перечисленных, но они на порядок сложнее. Для тех, кому интересно, приводим пример признака делимости на 11. Признак делимости на 11 +++++++++++++++++++++++++++++запомните!++++++++++++++++++++++++++++++++++++++ Число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11. ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++ В самом деле признак делимости на 11 очень интересен, попробуем разобраться на примере: Проверим, делится ли 671 на 11 . Признак делимости на 11 Итак, цифры которые стоят на нечетных местах - это 6 (стоит на первом месте) и 1 (стоит на третьим месте). Цифра, которая стоит на четном месте это 7 (стоит на втором месте). 6 + 1 = 7. Сумма цифр стоящих на нечетном месте равна сумме цифр на четном месте, значит 671 делится на 11. Проверим делится ли 3905 на 11 . Цифры которые стоят на нечетных местах - это 3 (стоит на первом месте) и 0 (стоит на третьим месте). Цифры, которые стоят на четном месте это 9 (стоит на втором месте) и 5 (стоит на четвертом месте). 3 + 0 ≠ 9 + 5 → 3 ≠ 14 Сумма цифр, стоящих на нечетном месте, не равна сумме цифр на четном месте, но суммы цифр отличаются ровно на 11. 14 - 3 = 11. Значит 3905 делится на 11. Яна Масловская: Добавлено спустя 6 минутМолодец, Юленька.Здрасти. Признаки делимости используются при решении уравнений в целых числах. Найти все целочисленные решения уравнения 16х+20у=14. Решение: Находим наибольший общий делитель 16 и 20; (16,20) = 4, а число 14 не делится на 4, то по теореме уравнение не имеет целочисленных решений. смотрите призентацияю в моём кабинете. Юлия Коленченко: Здравствуйте, сегодня я хочу рассказать несколько свойств делимости. 1.свойство делимости утверждает, что нуль делится на любое целое число b. Действительно, так как 0=b·0 для любого целого числа b, то нуль делится на любое целое число. В частности, нуль делится и на нуль. Это подтверждает равенство 0=0·q, где q – любое целое число. Из этого равенства вытекает, что частным от деления нуля на нуль является любое целое число. Также нужно отметить, что на 0 не делится никакое другое целое число a, отличное нуля. Поясним это. Если бы нуль делил целое число a, отличное от нуля, то должно было бы быть справедливо равенство a=0·q, где q – некоторое целое число, а последнее равенство возможно только при a=0. 2.Делимость обладает свойством транзитивности: если целое число a делится на некоторое целое число m, а число m в свою очередь делится на некоторое целое число b, то a делится на b. 3.Для любого целого и отличного от нуля числа b найдется такое целое число a, не равное b, которое делится на b. Таким числом будет любое из чисел a=b·q, где q – любое целое число, не равное единице. Можно переходить к следующему свойству делимости. Спасибо за внимение! |
||
|
#156 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 27
4099 дней назад
|
+2
Признаки делимости на 10,100,1000...
На 10 делятся числа которые оканчиваются на один 0. На 100,1000 и т.д такое же правило как и с 10, только надо прибавить несколько нолей к делимому. |
||
|
#157 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 30
4092 дня назад
|
+1
Здравствуйте я хочу представить задачу на делимость:
Для поездки с учениками за город школа заказала несколько одинаковых автобусов. 115 человек поехали на озеро, 138 - в лес. Все места в автобусах были заняты, и всем хватило места. Сколько было заказано автобусов и сколько мест в каждом автобусе? Ответ: Поскольку мест в автобусах не осталось, число детей, выехавших в каждом из двух направлений, кратно числу мест в автобусе. Следовательно, число мест в автобусе - общий делитель чисел 115 и 138. Для отыскания общего делителя воспользуемся правилом : общий делитель двух чисел является также общим делителем этих чисел и их разности. 138 - 115 = 23. Всего автобусов с детьми было : (115 + 138)/23 = 11 автобусов. |
||
|
#158 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 174
г.Комсомольск-на-Амуре
3929 дней назад
|
+1
Анечка, это справедливый факт и он может быть доказан в общем виде.
Аня Фахреева: Добавлено спустя 4 минутыСашуля, я не смогла рочитать условия задач-мелко.Здравствуйте.На уроке у Сергея Владимировича мне запомнился факт о делении чисел: возьмем,например число 25-это квадрат 5, количество делителей у него 3; число 4-это квадрат 2, количество делителей 3; число 49-квадрат 7, количество его делителей 3.Можно сделать вывод: количество делителей будет нечётным у чисел квадратов. |
||
|
#159 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 4
4106 дней назад
|
0
Счет Пети в банке содержит 500 долларов. Банк разрешает совершать только две операции :
1)Снимать 300 долларов 2)Добавлять 198 долларов Какую максимальную сумму может снять Петя в банке, если других денег у него нет? Решение: Так как НОД ( 300;198) = 6 Петя может снять сумму кратную 6 Попробуем подобрать такое число: 500-300+198-300+198+198= 494$... Проделав эти действия 16 раз Петя снимет 498$ |
||
|
#160 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 174
г.Комсомольск-на-Амуре
3929 дней назад
|
+1
Замечательная задача! Молодец, Илья!
Илья Михалев: Моя задачка на делимость: Коля и Вася живут в одном доме, на каждой лестничной клетке которого 4 квартиры. Коля живет на пятом этаже, в квартире 83, а Вася - на 3-ем этаже в квартире 169. Сколько этажей в доме ? Ответ :Если вести сквозной отсчет этажей, начиная с первого подъезда, то Коля живет на 21 этаже [83 : 4] = 20 (3). В своем подъезде Коля живет на 5 этаже, поэтому в подъездах, предшествующих Колиному, 16 этажей. 16 делится лишь на числа, кратные 2 поэтому в доме может быть либо 16 этажей, либо 8 этажей (вариант четырехэтажного дома исключаем, поскольку Коля живет на 5 этаже). Вася живет на 43 этаже, считая от первого этажа первого подъезда [169 : 4] = 42 (1). Значит в подъездах, предшествующих Васиному, 40 этажей. 40 делится на 8, но не делится на 16, следовательно, в доме 8 этажей. Замечание. В процессе решения задачи мы определили числа этажей (16 и 40) в двух разных группах подъездов. Число этажей в каждой группе подъездов кратно числу этажей в доме, оно равно произведению числа этажей в доме на число подъездов в группе. Задача сводится к нахождению общего делителя чисел 16 и 40 ( с уcловием, что делитель этот не меньше 5-ти). |
||
|
#161 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 4
4121 день назад
|
+1
здравствуйте я бы хотел выложить задачи на делимость Задача 7. Найти все пятизначные числа вида
517mn ( m, n - цифры), которые делятся на 18. Решение. Из того, что 18= 9 умножить на 2 получаем, что число 517mn должно делиться на 9 и на 2. Из признака делимости на 2 следует, что n - четная цифра, т.е. n= 0, 2, 4, 6, 8. Пусть n =0 , и числа имеют вид 517m0 . Из признака делимости на 9 следует делимость суммы 5 +1+ 7+ m+ 0 на 9. Следовательно, m может быть равным только 5. Получили число 51750. Пусть n= 2 , и числа имеют вид 517m2 . Из признака делимости на 9 следует делимость суммы 5 +1+ 7+ m+ 2 на 9. Следовательно, m может принимать только значение 3 и получается число 51732. Рассмотрев остальные варианты, аналогично находим остальные числа: 51714, 51786, 51768. Ответ: 51750, 51732, 51714, 51786, 51768. |
||
|
#162 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 5
4130 дней назад
|
+1
|
||
|
#163 - 8 октября 2014, среда
|
|||
|
Посетитель
Сообщений: 20
Комсомольск-на-Амуре
3933 дня назад
|
+1
Здравствуйте. Хочу рассказать как определить количество делителей у составного числа. Возьмём пример: 2 в 5-й степени умноженное 5 в 4-й. К показателям степени чисел прибавляем по 1 (5+1)*(4+1)=6*5=30. Ответ: 30 делителей у числа 2 в 5-й степени умноженное на 5 в 4-й.
|
||
|
#164 - 9 октября 2014, четверг
|
|||
|
Посетитель
Сообщений: 174
г.Комсомольск-на-Амуре
3929 дней назад
|
+1
молодец, Марина,нашла хорошую задачу.
Марина Чипизубова: Добавлено спустя 3 минутыКарина, а как звучит это правило в общем виде?Здравствуйте я хочу представить задачу на делимость: Для поездки с учениками за город школа заказала несколько одинаковых автобусов. 115 человек поехали на озеро, 138 - в лес. Все места в автобусах были заняты, и всем хватило места. Сколько было заказано автобусов и сколько мест в каждом автобусе? Ответ: Поскольку мест в автобусах не осталось, число детей, выехавших в каждом из двух направлений, кратно числу мест в автобусе. Следовательно, число мест в автобусе - общий делитель чисел 115 и 138. Для отыскания общего делителя воспользуемся правилом : общий делитель двух чисел является также общим делителем этих чисел и их разности. 138 - 115 = 23. Всего автобусов с детьми было : (115 + 138)/23 = 11 автобусов. Карина Юртикова: Добавлено спустя 4 минутыХорошая задача,Никита!Здравствуйте. Хочу рассказать как определить количество делителей у составного числа. Возьмём пример: 2 в 5-й степени умноженное 5 в 4-й. К показателям степени чисел прибавляем по 1 (5+1)*(4+1)=6*5=30. Ответ: 30 делителей у числа 2 в 5-й степени умноженное на 5 в 4-й. Никита Кобяков: здравствуйте я бы хотел выложить задачи на делимость Задача 7. Найти все пятизначные числа вида 517mn ( m, n - цифры), которые делятся на 18. Решение. Из того, что 18= 9 умножить на 2 получаем, что число 517mn должно делиться на 9 и на 2. Из признака делимости на 2 следует, что n - четная цифра, т.е. n= 0, 2, 4, 6, 8. Пусть n =0 , и числа имеют вид 517m0 . Из признака делимости на 9 следует делимость суммы 5 +1+ 7+ m+ 0 на 9. Следовательно, m может быть равным только 5. Получили число 51750. Пусть n= 2 , и числа имеют вид 517m2 . Из признака делимости на 9 следует делимость суммы 5 +1+ 7+ m+ 2 на 9. Следовательно, m может принимать только значение 3 и получается число 51732. Рассмотрев остальные варианты, аналогично находим остальные числа: 51714, 51786, 51768. Ответ: 51750, 51732, 51714, 51786, 51768. |
||
|
#165 - 9 октября 2014, четверг
|
|||
|
Посетитель
Сообщений: 9
Комсомольск - на - Амуре
4101 день назад
|
+1
Я задам несколько задач на делимость.
Дано пятизначное число 25762. Какую цифру и на каком месте надо дописать, чтобы полученное число делилось на 36 ? Ответ: Искомое число делится на 4 и 9. Дописав к данному числу цифру 5, получим число, кратное 9-ти. Чтобы полученное число делилось на 4, цифру 5 допишем в разделе десятков. Искомое число - 257652. Найдите наименьшее натуральное число, которое при делении на 7 дает в остатке 6, а при делении на 9 остаток равен 8.. В обоих случаях - как при делении искомого числа на 7, так и при делении его на 9 остаток на единицу меньше делителя. Увеличив делимое на 1, получим число, которое делится без остатка и на 7, и на 9. Наименьшее такое число - 63. Искомое число на 1 меньше и равно 62. |
||
Быстрый ответ
Чтобы писать на форуме, зарегистрируйтесь или авторизуйтесь.
 Центр поддержки одаренных детей ХКИРО
Центр поддержки одаренных детей ХКИРО