Центр поддержки одаренных детей ХКИРО

Я нашла одну интересную задачу:

Теплоход «Суворов» свой рейс туда и обратно совершает за 8 дней, теплоход «Москва» - за 12 дней, а теплоход «Киров» - за 18 дней. Через сколько дней теплоходы снова встретятся в порту, если ушли в рейс одновременно?

Ответ: Через 36 дней, т. к. Суворов тратит на дорогу в один конец - 4 дня, Горький - 6 дней, Киров - 9 дней. Наименьшее общее кратное - 36, следовательно они встретятся через это время.

Задачи на делимость чисел

1. Найдите наименьшее число, которое при делении на 2 дает остаток 1, при делении на 3 — 2, на 4 — 3, на 5 — 4, на 6 — 5, на 7 — 6, на 8 — 7, на 9 — 8, на 10 — 9.

2. Найти все числа, большие 25000, но меньшие 30000, которые как при делении на 131, так и при делении на 1965 дают в остатке 125.

3. При делении некоторого числа на 225 в остатке получилось 150. Разделится ли данное число на 75 и почему?Добавлено спустя несколько секундПризнаки делимости чисел:
Число делится на 2, если на 2 делится его последняя цифра.
Число делится на 3, если на 3 делится сумма его цифр.
Число делится на 4, если на 4 делится число, составленное из последних двух цифр.
Число делится на 5, если на 5 делится его последняя цифра.
Число делится на 6, если на 2 делится его последняя цифра, и делится на 3 сумма цифр (т.е. комбинация признаков на 2 и 3).
Число делится на 8, если на 8 делится число, составленное из последних трех цифр.
Число делится на 9, если на 9 делится сумма его цифр.
Число делится на 10, если последняя цифра числа – 0.
Число делится на 72, если на 8 делится число, составленное из последних трех цифр, и делится на 9 сумма цифр (т.е. комбинация признаков на 8 и 9, т.к. 72=8*9).

Можно ли число 1980 поровну разделить на 3 равные части используя любые знаки и только числа которые я написал - 90(2 шт), 170(7 шт), 19(19 шт), 2(80 шт).

Ответ: невозможно.

1 день-изготовили 246 дет.
2 день-изготовили в 2 раза меньше
3 день-изготовили столько деталей, сколько было изготовлено в 1-ом и во 2-ом дне.
4 день- рабочие потрудились и изготовили столько, сколько изготовили за все 3- дня.
Вопрос: Сколько изготовили в 4-ый день?

1) 246:2=123(дет) изготовили во 2-ой день
2) 246+123=369(дет) изготовили в 3-ий день
3) 246+396+123=765(дет)
Ответ: в 4-ый день изготовили 765 деталей.

Sofya Chugay, хорошо
Даниэла Фисенко, повтор задач и нет решений
макар плотников, нет решения Сергей Трутнев,задача не по темеДобавлено спустя 4 минутыРенат Романчук, хорошо Карина Юртикова, Саша Вагина,повтор задач

Мои задачки на делимость:
Задача 1:
а) a + 1 делится на 3. Докажите, что 4 + 7a делится на 3.
б) 2 + a и 35 – b делятся на 11. Докажите, что a + b делится на 11.


Решение:
а) 4 + 7a = 4(a + 1) + 3a;
б) a + b = (2 + a) – (35 – b) + 33.

Наталья Леонидовна, я сделала до конца работу.Посмотрите , у меня в виде презентации и документа
При́знак дели́мости — алгоритм, позволяющий сравнительно быстро определить, является ли число кратным заранее заданному[1]. Если признак делимости позволяет выяснить не только делимость числа на заранее заданное, но и остаток от деления, то его называют признаком равноостаточности.

Признак делимости на 10, 100 и 1000
На 10 делятся нацело только те числа, последняя цифра которых нуль.
На 100 делятся нацело только те числа, две последние цифры которых нули.
На 1000 делятся нацело только те числа, три последние цифры нули.
Чтобы было проще делить на 10, 100 и 1000, просто зачеркивайте одинаковое количество нулей в обоих числах.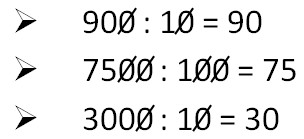
Примеры:Добавлено спустя 14 минутПризнак делимости на 11
Число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11.

В самом деле признак делимости на 11 очень интересен, попробуем разобраться на примере:
Проверим, делится ли 671 на 11 .

Итак, цифры которые стоят на нечетных местах - это 6 (стоит на первом месте) и 1 (стоит на третьим месте). Цифра, которая стоит на четном месте это 7 (стоит на втором месте). 6 + 1 = 7. Сумма цифр стоящих на нечетном месте равна сумме цифр на четном месте, значит 671 делится на 11.

Проверим делится ли 3905 на 11
Цифры которые стоят на нечетных местах - это 3 (стоит на первом месте) и 0 (стоит на третьим месте). Цифры, которые стоят на четном месте это 9 (стоит на втором месте) и 5 (стоит на четвертом месте).

3 + 0 ≠ 9 + 5 → 3 ≠ 14 Сумма цифр, стоящих на нечетном месте, не равна сумме цифр на четном месте, но суммы цифр отличаются ровно на 11. 14 - 3 = 11. Значит 3905 делится на 11.

Вот мои задачи на делимость:
Два класса с одинаковым количеством учеников написали контрольную. Проверив контрольные, строгий директор Фёдор Калистратович сказал, что он поставил двоек на 13 больше, чем остальных оценок. Не ошибся ли строгий Фёдор Калистратович.
Решение:
Конечно же, Фёдор Калистратович ошибся. Число оценок должно быть чётным, поскольку чётно число учеников, но если бы Фёдор Калистратович был прав, то число учеников можно было бы выразить формулой 13 + 2a, где a — число "не двоек", т.е. получается, что число учеников нечётно. Противоречие и доказывает, что Фёдор Калистратович был неправ.
Ответ:Федор Калистратович ошибся

Ваня задумал простое трёхзначное число, все цифры которого различны. На какую цифру оно может оканчиваться, если его последняя цифра равна сумме первых двух?
Решение:
Очевидно, что последняя цифра больше 1. Трёхзначное простое число не может оканчиваться ни на чётную цифру (т. е. на 0, 2, 4, 6 или 8), ни на цифру 5. Если последняя цифра 3 или 9, то сумма всех цифр числа, равная удвоенной последней цифре, делится на 3, а тогда само число делится на 3. Таким образом, осталась только цифра семь.

Егор Файзуллин, молодец

Дмитрий Александров, молодец

Про семь натуральных чисел известно, что сумма любых шести из них делится на 5. Докажите, что каждое из данных чисел делится на 5.


Решение:

Докажите, что любые два числа из этих семи дают одинаковый остаток от деления на 5. Для этого рассмотрите две шестерки: одну – не содержащую первое из них, вторую – не содержащую второе.

Сколько существует натуральных чисел, меньших 1000, которые не делятся ни на 5 ни на 7?

Решение:Среди 999 чисел, меньших 1000,
199 чисел кратны 5 : [999 : 5] = 199 *.
В этом же интервале имеются 142 числа, кратных 7 : [999 : 7] = 142* .

Среди 142 чисел, кратных 7, имеются числа, которые делятся также и на 5, то есть кратные 35.

Всего таких чисел 28: [999 : 35]= 28* .

Эти 28 чисел уже учтены в числе 199, найденном ранее.

Поэтому количество чисел, меньших 1000, которые делятся либо на 5, либо на 7, равно 199 + 142 - 28 = 313.

В рассматриваемом интервале остается 999 - 313 = 686 чисел,
которые не делятся ни на 5, ни на 7.

Полученное число делится на 27?

Какую цифру нужно приписать к числу 97 справа и слева, чтобы полученное число делилось на 27?

Удвоенная неизвестная цифра дополняет сумму известных цифр числа до величины, кратной 9-ти.
Сумма известных чисел - четная (16). Удвоенная неизвестная цифра (a) - также четная величина.
Следовательно, сумма цифр искомого числа - четная и равна 18-ти. (2a меньше или равна 18 и сумма цифр искомого числа не больше 34-х).

Итак, a = 1, искомое число - 1971.

Васильева Софья, Костя Андоськин, Никита Киселёв, вы подобрали хорошие задачи. Хорошо будет,если сумеете их рассказать классу

Наталья Леонидовна, я сделала до конца работу.Посмотрите , у меня в виде презентации и документа