математики перешли на новый уровень
|
#211 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 174
г.Комсомольск-на-Амуре
3929 дней назад
|
0
Арина Демидова, задача простовата, такие есть в школьном учебникеДобавлено спустя 1 минутуДмитрий Александров, хорошо.
|
|
#212 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 6
4107 дней назад
|
+1
Для поездки с учениками за город школа заказала несколько одинаковых автобусов.
115 человек поехали на озеро, 138 - в лес. Все места в автобусах были заняты, и всем хватило места. Сколько было заказано автобусов и сколько мест в каждом автобусе ? |
|
#213 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 11
4115 дней назад
|
0
Задача на деление
Целое число кратно 11 и при делении на пять даёт остаток 3. Найдите остаток от деления этого числа на 55. 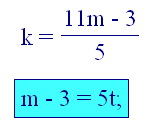 |
|
#214 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 1
4120 дней назад
|
+2
Всем привет, я бы хотела поделиться задачей на делимость!
 Найдите наименьшее натуральное число, которое при делении на 7 даёт в остатке 6, а при делении на 9 остаток равен 8. Решение: В этих двух случаях как при делении неизвестного числа на 7 так и на 9 остаток на единицу меньше делителя, так что если мы увеличим делимое на один то оно будет делиться без остатка на 7 и 9. НОК(7 и 9) = 63; 63-1= 62- это и будет неизвестное число.Добавлено спустя 11 минутА вот ещё одна задача!!! Дано пятизначное число 25762. Какую цифру и на каком месте надо дописать, чтобы полученное число делилось на 36? Решение: Неизвестное число делится на 4 и 9 так как, 4*9=36. Если подписать к числу цифру 5, мы получим число кратное девяти. А чтобы полученное число делилось на 4,то 5 мы будем писать в разделе десятков, и тогда неизвестное число будет 257652. |
|
#215 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 13
Комсомольск - на - Амуре
4120 дней назад
|
+1
1)Число яблок в ящике меньше 200. Их можно разделить поровну между 2,3,4,5,6 детьми. Какое максимальное количество яблок может быть в ящике?
Решение: НОК ( 2,3,4,5,6) = 60. 60х < 200, значит максимальное количество в ящике 180 яблок. Ответ: 180 яблок. 2)Сколько в корзине яиц, если их число одновременно делится на 2, на 3, на 5, на 10, на 15? Решение: НОК ( 2,3,5,10,15) = 60. Ответ: 60 яиц. |
|
#216 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 27
4099 дней назад
|
0
Сколько максимум поместится арбузов по 4 кг в 5 грузовиков, 1 вмещает 4 тонны, 2- 8000000 грамм, 3- 10000 килограмм, 4- 1000 центнеров, 5- 1000000000000 миллиграмм.
|
|
#217 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 174
г.Комсомольск-на-Амуре
3929 дней назад
|
0
Елизавета Павлова, такая задача былаДобавлено спустя 2 минутымакар плотников, нет решенияДобавлено спустя 4 минутыДанил Вашковец, хорошо Рита Леонова, отличноДобавлено спустя 5 минутНина Молочкова, мне непонятно.А тебе?
|
|
#218 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 24
3911 дней назад
|
0
Здравствуйте!вот моя задача
У марсиан Бывает произвольное число рук. Днажды все марсиан взяли за руки так,что свободных рук не осталось. Докажите что у марсиан,нечетное число рук,четно. Ответ: т.к свободных рук не осталось,то общее число рук четно . Более число рук у марсиан с четным числом всегда четно,а у марсиан с нечетным числом рук общее число будет только тогда,когда марсиан четное число |
|
#219 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 4
4101 день назад
|
0
Задача на делимоть :
1.Найдите наименьшее число, дающее следующие остатки: 1 – при делении на 2, 2 – при делении на 3, 3 – при делении на 4, 4 – при делении на 5, 5 – при делении на 6. Заметим, что это число, увеличенное на 1, делится на 2, 3, 4, 5, 6. Ответ: 59.Добавлено спустя 7 минутЗадача 2 : Назовем автобусный билет счастливым если сумма цифр его шестизначного номера делится на 13. могут ли 2 идущих подряд билета оказаться счастливым? Ответ: признак делимости на 7 или 13: разбиваем десятичную запись числа справа налево по 3 цифры в каждой (самая левая группа может содержать 2или 1 цифру) . Взять группы с нечетными номерами со знаком минус, а с четными со знаком плюс. Если значение получившегося выражения делится на 7(13), то и число делится на 7(13).Добавлено спустя 11 минутЗадача 3 : На некотором острове необычайно регулярный климат : по понедельникам и средам всегда идут дожди,по субботам - туман, зато в остальные дни - солнечно.Утром какого дня недели нужно начать свой отдых группе туристов, если они хотят пробыть там 44 дня и захватить при этом как можно больше солнечных дней? A - в понедельник; B - в среду; C - в четверг; D - в пятницу; E - во вторник Решение :Выясним, сколько полных недель в 44 днях. Получим 6 недель. В течении этих недель число солнечных дней не зависит от того, когда начнется отдых. В качестве оставшихся двух дней выбираем четверг и пятницу - солнечные дни.Следовательно, отправляем туристов утром в четверг. То есть верный ответ - (С).Добавлено спустя 12 минутЗадача 4 : Остаток от деления 100 на некоторое число равен 4. При делении 90 на это же число в остатке получается 18. На какое число делили? A - 18; B - 32; C - 24; D - 36; A - 48; Решение : Из условия следует, что 100-4=96 делится на искомое число. Также 90-18=72 делится на искомое число. Их разность также делится на искомое число: 96-72=24. Следовательно, искомое число - 24, так как на него делится и 96, и 72. Верен ответ (С). |
|
#220 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 14
4102 дня назад
|
0
Моя задача
на делимость: Среди 999 чисел, меньших 1000, 199 чисел кратны 5 : [999 : 5] = 199 *. В этом же интервале имеются 142 числа, кратных 7 : [999 : 7] = 142* . Среди 142 чисел, кратных 7, имеются числа, которые делятся также и на 5, то есть кратные 35. Всего таких чисел 28: [999 : 35]= 28* . Эти 28 чисел уже учтены в числе 199, найденном ранее. Поэтому количество чисел, меньших 1000, которые делятся либо на 5, либо на 7, равно 199 + 142 - 28 = 313. В рассматриваемом интервале остается 999 - 313 = 686 чисел, которые не делятся ни на 5, ни на 7.Добавлено спустя 5 минутЕщё одна интересная задачка:Женщина несла на базар корзину яиц. Прохожий нечаянно толкнул женщину, корзина упала и яйца разбились. Виновник несчастья, желая возместить потерю, поинтересовался, сколько яиц было в корзине. - Точно не помню, ответила женщина, - но знаю, что когда я вынимала из корзины по 2, по 3, по 4, по 5, по 6 яиц, в корзине оставалось одно яйцо, а когда я вынимала по 7, в корзине ничего не оставалось. Сколько яиц было в корзине ? Если бы из корзины вынули одно яйцо, оставшееся количество яиц делилось бы нацело на 2, 3, 4, 5, и 6. Числа, для которых это выполняется, - это 60 и числа, кратные 60-ти. Задача сводится к нахождению числа, кратного 60-ти, которое делилось бы на 7 после добавления 1 ( или, иными словами, при делении на 7 давало бы остаток 6). Число 60 при делении на 7 дает остаток 4. Следовательно, нужно найти число, кратное 4-ем, которое было бы на 6 больше числа, кратного 7-ми. Это число - остаток от деления общего числа яиц на 7, оно равно 7· 2 +6 = 20. ** В этом числе остаток 4 содержится пятикратно, значит, первоначально в корзине было 60 · 5 + 1 = 301 яйцо. Редактировалось: 1 раз (Последний: 22 октября 2014 в 20:10)
|
|
#221 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 1
4120 дней назад
|
+1
Здравствуйте! Вот мои задачи
1) 2 + a и 35 – b делятся на 11. Докажите, что a + b делится на 11. Решение: a + b = (2 + a) – (35 – b) + 33. 2) Про семь натуральных чисел известно, что сумма любых шести из них делится на 5. Докажите, что каждое из данных чисел делится на 5. Решение: Докажите, что любые два числа из этих семи дают одинаковый остаток от деления на 5. Для этого рассмотрите две шестерки: одну – не содержащую первое из них, вторую – не содержащую второе. 3) В миске лежали апельсины. Сколько в миске апельсинов если их число одновременно делиться на 3, на 5, на 15, на 30,на 45. Решение: НОК( 3,5,15,30,45)=270. |
|
#222 - 22 октября 2014, среда
|
|
|
Посетитель
Сообщений: 1
4120 дней назад
|
+1
Посчитаем черепашек на Олимпийских Играх Зверей!
В команде рептилий были только черепашки. Черепашек было больше 50-ти, но меньше 100. На церемонии открытия Олимпийских Игр Зверей эту команду никак не удавалось построить рядами по 2, 3, или 4 животных, так как одного животного всегда не хватало в последнем ряду. Поэтому пришлось построить команду черепашек рядами по 5 животных в каждом ряду. Сколько всего черепашек было в команде рептилий? Ответ:Если искомое число черепашек увеличить на 1, оно будет делиться на 2, 3, 4. Наименьшее общее кратное этих чисел 12. Возьмем под подозрение числа, кратные 12, большие 50 и меньшие 100. Это будут числа: 60, 72, 84 и 96. Искомое число должно быть на 1 меньше указанных чисел и делиться на 5. Из нашего ряда подходит только число 96, так как: 96 - 1 = 95, получаем число, делящееся на 5. Итак, 95 черепашек было в команде рептилий.Добавлено спустя 8 минутСколько существует натуральных чисел, меньших 1000, которые не делятся ни на 5 ни на 7? Ответ: Среди 999 чисел, меньших 1000, 199 чисел кратны 5 : [999 : 5] = 199 *. В этом же интервале имеются 142 числа, кратных 7 : [999 : 7] = 142* . Среди 142 чисел, кратных 7, имеются числа, которые делятся также и на 5, то есть кратные 35. Всего таких чисел 28: [999 : 35]= 28* . Эти 28 чисел уже учтены в числе 199, найденном ранее. Поэтому количество чисел, меньших 1000, которые делятся либо на 5, либо на 7, равно 199 + 142 - 28 = 313. В рассматриваемом интервале остается 999 - 313 = 686 чисел, которые не делятся ни на 5, ни на 7. * [N] - целая часть числа N . Например, [13,45] = 13. |
|
#223 - 23 октября 2014, четверг
|
|
|
Посетитель
Сообщений: 174
г.Комсомольск-на-Амуре
3929 дней назад
|
0
София Бабина, такая задача былаДобавлено спустя 2 минутыГалина Корендясова, хорошо, Ренат Романчук, нет решений.
|
|
#224 - 23 октября 2014, четверг
|
|
|
Посетитель
Сообщений: 20
Комсомольск-на-Амуре
3933 дня назад
|
+1
Женщина несла на базар корзину яиц.
Прохожий нечаянно толкнул женщину, корзина упала и яйца разбились. Виновник несчастья, желая возместить потерю, поинтересовался, сколько яиц было в корзине. - Точно не помню, ответила женщина, - но знаю, что когда я вынимала из корзины по 2, по 3, по 4, по 5, по 6 яиц, в корзине оставалось одно яйцо, а когда я вынимала по 7, в корзине ничего не оставалось. Сколько яиц было в корзине ? Решение: Если бы из корзины вынули одно яйцо, оставшееся количество яиц делилось бы нацело на 2, 3, 4, 5, и 6. Числа, для которых это выполняется, - это 60 и числа, кратные 60-ти. Задача сводится к нахождению числа, кратного 60-ти, которое делилось бы на 7 после добавления 1 ( или, иными словами, при делении на 7 давало бы остаток 6). Число 60 при делении на 7 дает остаток 4. Следовательно, нужно найти число, кратное 4-ем, которое было бы на 6 больше числа, кратного 7-ми. Это число - остаток от деления общего числа яиц на 7, оно равно 7· 2 +6 = 20. ** В этом числе остаток 4 содержится пятикратно, значит, первоначально в корзине было 60 · 5 + 1 = 301 яйцо. ** Замечание. Следующее, большее число, обладающее указанным свойством, равно 7 · 6 + 6 = 48. Такой остаток может быть получен при 12-кратном повторении порции 60 яиц (48 : 4 = 12). В этом случае, число яиц в корзине составило бы 60 · 12 + 1 = 721 яйцо - вариант, в рассматриваемой ситуации нереальный. Такую корзину женщине не поднять. |
|
#225 - 23 октября 2014, четверг
|
|
|
Посетитель
Сообщений: 16
4119 дней назад
|
+1
Женщина несла на базар корзину яиц.
Прохожий нечаянно толкнул женщину, корзина упала и яйца разбились. Виновник несчастья, желая возместить потерю, поинтересовался, сколько яиц было в корзине. - Точно не помню, ответила женщина, - но знаю, что когда я вынимала из корзины по 2, по 3, по 4, по 5, по 6 яиц, в корзине оставалось одно яйцо, а когда я вынимала по 7, в корзине ничего не оставалось. Сколько яиц было в корзине ? Если бы из корзины вынули одно яйцо, оставшееся количество яиц делилось бы нацело на 2, 3, 4, 5, и 6. Числа, для которых это выполняется, - это 60 и числа, кратные 60-ти. Задача сводится к нахождению числа, кратного 60-ти, которое делилось бы на 7 после добавления 1 ( или, иными словами, при делении на 7 давало бы остаток 6). Число 60 при делении на 7 дает остаток 4. Следовательно, нужно найти число, кратное 4-ем, которое было бы на 6 больше числа, кратного 7-ми. Это число - остаток от деления общего числа яиц на 7, оно равно 7· 2 +6 = 20. ** В этом числе остаток 4 содержится пятикратно, значит, первоначально в корзине было 60 · 5 + 1 = 301 яйцо. |
Быстрый ответ
Чтобы писать на форуме, зарегистрируйтесь или авторизуйтесь.
 Центр поддержки одаренных детей ХКИРО
Центр поддержки одаренных детей ХКИРО