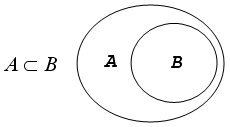
На диаграмме кругов Эйлера видно, что A является подмножеством B, а B является надмножеством A.
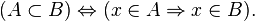
Числа, делящиеся на 9.
9 групп чисел вида 9n; 9n+1; 9n+2; 9n+3; 9n+4; 9n+5; 9n+6; 9n+7; 9n+8.
где n- натурально
|
#76 - 21 сентября 2014, воскресенье
|
|
|
Посетитель
Сообщений: 71
Комсомольск-на-Амуре
4059 дней назад
|
+1
Подмно́жество в теории множеств — это понятие части множества.
На диаграмме кругов Эйлера видно, что A является подмножеством B, а B является надмножеством A.  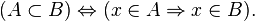 Числа, делящиеся на 9. 9 групп чисел вида 9n; 9n+1; 9n+2; 9n+3; 9n+4; 9n+5; 9n+6; 9n+7; 9n+8. где n- натурально |
|
#77 - 21 сентября 2014, воскресенье
|
|
|
Посетитель
Сообщений: 10
4098 дней назад
|
+2
Я предлагаю разделить числа на:
1. Числа состоящие из одной и той же цифры. Пример: 222, 4444, 66 и т.д. 2. Числа состоящие из разных цифр. Пример: 228, 1488, 2014 и т.д. |
|
#78 - 22 сентября 2014, понедельник
|
|
|
Посетитель
Сообщений: 174
г.Комсомольск-на-Амуре
3929 дней назад
|
0
Яночка, депящиеся на 9-это числа вида 9а (делятся нацело)
Ты разбила правильно на группы по остаткам от деления на 9. Согласна? Яна Масловская: Добавлено спустя 2 минутыХорошая информацияЗдравствуйте. я сегодня расскажу на какие подмножества можно разложить множество натуральных чисел. Можно разделить на группы делящиеся на "9" 9n; 9n+1; 9n+2; 9n+3; 9n+4; 9n+5; 9n+6; 9n+7; 9n+8.  Также можно разделить на "10"  10m; 10m+1; 10m+2; 10m+3; 10m+4; 10m+5; 10m+6; 10m+7; 10m+8; 10m+9. на сегодня у меня пока всё, До свидания.  Марина Чипизубова: Марина очень хороший вариант. Здравствуйте!!! Я расскажу на какие подмножества можно разложить множество натуральных чисел. Можно разложить на числа которые кратны 5 и не кратны 5  Кратны 7 и не кратны 7  И еще множество других подмножеств  Евфросиния Анисимова: Добавлено спустя 4 минутыМолодец,понимаешь правильно,только второе множество надо почетче охарактеризовать.Подмно́жество в теории множеств — это понятие части множества. На диаграмме кругов Эйлера видно, что A является подмножеством B, а B является надмножеством A.  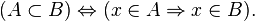 Числа, делящиеся на 9. 9 групп чисел вида 9n; 9n+1; 9n+2; 9n+3; 9n+4; 9n+5; 9n+6; 9n+7; 9n+8. где n- натурально Никита Киселёв: Я предлагаю разделить числа на: 1. Числа состоящие из одной и той же цифры. Пример: 222, 4444, 66 и т.д. 2. Числа состоящие из разных цифр. Пример: 228, 1488, 2014 и т.д. |
|
#79 - 22 сентября 2014, понедельник
|
|
|
Посетитель
Сообщений: 4
4106 дней назад
|
+1
Я предлагаю разделить числа на 4 множества
1) от 1 до 7: 1,2,3,4,5,6,7 2) от 7 до 15: 8,9,10,11,12,13,14,15 3) от 15 до 100 : 16,17,18... 4) от 100 до бесконечности : 100,101... |
|
#80 - 22 сентября 2014, понедельник
|
|
|
Посетитель
Сообщений: 23
4102 дня назад
|
+2
я предогаю разделить натуральные числа на дружиственные и не дружественые .
Напоминание что такое дружественные числа :Дружественные числа — два различных натуральных числа, для которых сумма всех собственных делителей первого числа равна второму числу и наоборот, сумма всех собственных делителей второго числа равна первому числу. Иногда частным случаем дружественных чисел считаются совершенные числа: каждое совершенное число дружественно себе. Дружественные числа изобрёл Пифагор. |
|
#81 - 22 сентября 2014, понедельник
|
|
|
Посетитель
Сообщений: 4
4102 дня назад
|
+1
Здравствуйте!
Я хочу показать вам , на какие группы можно разделить множество натуральных чисел. Я разделил на 3 группы : это числа вида 3n , 3n+1 , и 3n+2 , если n - натуральное число. |
|
#82 - 22 сентября 2014, понедельник
|
|
|
Посетитель
Сообщений: 7
4102 дня назад
|
+1
Здравствуйте.
Я хочу показать на какие еще группы можно разделить натуральные числа. Круглые и не круглые. круглые:20 10 300... не круглые:25 112 5555... |
|
#83 - 23 сентября 2014, вторник
|
|
|
Посетитель
Сообщений: 174
г.Комсомольск-на-Амуре
3929 дней назад
|
0
Алиса,замечательный пример ,только слова "включительно" не хватает;ркчь о числах 7,15 и100 в 3 местах
Алиса Казелько: Добавлено спустя 1 минутуХороший пример.Я предлагаю разделить числа на 4 множества 1) от 1 до 7: 1,2,3,4,5,6,7 2) от 7 до 15: 8,9,10,11,12,13,14,15 3) от 15 до 100 : 16,17,18... 4) от 100 до бесконечности : 100,101... Александра Дружинина: Добавлено спустя 2 минутыПаша,был уже такой примеря предогаю разделить натуральные числа на дружиственные и не дружественые . Напоминание что такое дружественные числа :Дружественные числа — два различных натуральных числа, для которых сумма всех собственных делителей первого числа равна второму числу и наоборот, сумма всех собственных делителей второго числа равна первому числу. Иногда частным случаем дружественных чисел считаются совершенные числа: каждое совершенное число дружественно себе. Дружественные числа изобрёл Пифагор. Павел Постнов: Здравствуйте. Я хочу показать на какие еще группы можно разделить натуральные числа. Круглые и не круглые. круглые:20 10 300... не круглые:25 112 5555... |
|
#84 - 23 сентября 2014, вторник
|
|
|
Посетитель
Сообщений: 25
Комсомольск-на-Амуре
4079 дней назад
|
+2
всем привет
числа можно разбить на много разных групп а вот такое разделение как а=5n a=5n+1 a=5n+2 a=5n+3 a=5n+4 можно провести с любым числом:9,20,34, и т.д. до бесконечности |
|
#85 - 23 сентября 2014, вторник
|
|
|
Посетитель
Сообщений: 5
4130 дней назад
|
+1
Здравствуйте сегодня я расскажу вам про подмножества чисел.
Подмножества - множество являющейся частью другого множества. Можно создать подмножество - это числа например делящиеся на 2. Так же можно создать другие подмножества это числа которые делятся на 3,4,5,6,7,8,9,10 и так далее. И тем самым можно создать без конечное количество подмножеств. Редактировалось: 2 раза (Последний: 23 сентября 2014 в 14:44)
|
|
#86 - 23 сентября 2014, вторник
|
|
|
Посетитель
Сообщений: 4
4101 день назад
|
+1
Я предлагаю разделить числа на
1 группа : 1-ые,2-ые,3-ые,4-ые,5-ые. 2 группа : 6-ые,7-ые,8-ые.....Добавлено спустя 2 минутыИли разделить на 1 группа : В числах которых есть цифра 5. 2 группа: В числах которых нет цифры 5. |
|
#87 - 23 сентября 2014, вторник
|
|
|
Посетитель
Сообщений: 21
4101 день назад
|
+1
Я предлагаю разбить числа на 5 групп:
1.Числа последняя цифра которых является 1 2.Числа последняя цифра которых является 3 3.Числа последняя цифра которых является 5 4.Числа последняя цифра которых является 7 5. Все остальные Редактировалось: 1 раз (Последний: 23 сентября 2014 в 17:37)
|
|
#88 - 23 сентября 2014, вторник
|
|
|
Посетитель
Сообщений: 174
г.Комсомольск-на-Амуре
3929 дней назад
|
0
Правильно
Костя Андоськин: Добавлено спустя 4 минутыНеля,ты имеешь в виду Я предлагаю разбить числа на 10 групп. 1 группа это те числа которые делятся на 10 без остатка. Потом группы чисел по возрастанию остатка, например: m+1,m+2,m+3.....m+9 однозначные двузначначные трехзначные и т.д? Неличка Кириченко: Добавлено спустя 5 минутОригинально. Молодец.Я предлагаю разделить числа на 1 группа : 1-ые,2-ые,3-ые,4-ые,5-ые. 2 группа : 6-ые,7-ые,8-ые..... Или разделить на 1 группа : В числах которых есть цифра 5. 2 группа: В числах которых нет цифры 5. Булгакова Елизавета: Добавлено спустя 11 минутЛеша, у тебя правильное понимание понятия подмножества.Но надо разбить множество натуральных чисел на 2-3 множества.Я предлагаю разбить числа на 5 групп: 1.Числа последняя цифра которых является 1 2.Числа последняя цифра которых является 3 3.Числа последняя цифра которых является 5 4.Числа последняя цифра которых является 7 5. Все остальные Алексей Паненко: Здравствуйте сегодня я расскажу вам про подмножества чисел. Подмножества - множество являющейся частью другого множества. Можно создать подмножество - это числа например делящиеся на 2. Так же можно создать другие подмножества это числа которые делятся на 3,4,5,6,7,8,9,10 и так далее. И тем самым можно создать без конечное количество подмножеств. |
|
#89 - 24 сентября 2014, среда
|
|
|
Посетитель
Сообщений: 4
4102 дня назад
|
+1
Множество Q - множество рациональных чисел (это целые числа, либо числа, которые представимы в виде дроби, в числителе и знаменателе которой целые числа. Десятичная запись рациональных либо конечна, либо представима в виде дроби, в которой обязательно есть периодическое повторение).
Множество Z - множество целых чисел (это натуральные, ноль, и целые отрицательные). |
|
#90 - 25 сентября 2014, четверг
|
|
|
Посетитель
Сообщений: 174
г.Комсомольск-на-Амуре
3929 дней назад
|
0
Василиса, перечитай внимательно мое задание.
Василиса Копылова: Множество Q - множество рациональных чисел (это целые числа, либо числа, которые представимы в виде дроби, в числителе и знаменателе которой целые числа. Десятичная запись рациональных либо конечна, либо представима в виде дроби, в которой обязательно есть периодическое повторение). Множество Z - множество целых чисел (это натуральные, ноль, и целые отрицательные). |