Математика

Елизавета Воронова

Посетитель

Сообщений: 25

Комсомольск-на-Амуре

3673 дня назад

0

Ответ:

Прикрепленные файлы:

zadachka_53706ca50bcb9.gif | 12,12 Кб | Скачали: 1348 раз

Наталья Леонидовна Будлянская

Посетитель

Сообщений: 174

г.Комсомольск-на-Амуре

3523 дня назад

0

Саша,у тебя разве про куб задачи?проверь свой заголовок

Александра Дружинина:

Задача на куб и его S:
№1
как изменится площадь квадрата если его сторону увеличить в 2 раза ?
Ответ : площадь плоских фигур при увеличении их сторон в икс раз увеичивается в икс*икс раз
№2
Вадим разрезал квадратный листок бумаги со стороной 8 см на два прямоугольника. Периметр одного из этих прямоугольников равен 22 см. Чему равна площадь другого?
решение: Нарисуем квадрат. Что мы знаем о квадратах? У квадрата все стороны равны. В нашем случае все стороны квадрата равны 8 см. Если Вадим отрезал у квадрата какую-то часть – то квадрат превращается в два прямоугольника, длинные стороны которого имеют величину 8 см.

Что нам известно еще? Нам известен периметр одного из прямоугольников и также мы выяснили, что длинная сторона этого прямоугольника равна 8 см. Следовательно, мы можем без труда вычислить другие две стороны прямоугольника. Периметр прямоугольника – это сумма длин всех его сторон:

22=8+8+X+X
X = (22 - 16) : 2 = 6 : 2 = 3 (см)

Мы узнали, что один из отрезанных прямоугольников имеет стороны 8 см и 3 см. Значит теперь можно найти стороны неизвестного прямоугольника. Дело в том, что когда квадрат не был разрезан – его стороны были по 8 см. Но потом от одной из сторон в 8 см отрезали 3 см. Значит, мы можем найти неизвестную сторону другого прямоугольника:

8 – 3 = 5 (см)

В задаче поставлен вопрос – найти площадь прямоугольника. Площадь прямоугольника можно узнать, перемножив ширину на длину, т. е.
8 x 5 = 40 (см)

Зачатую в задачах спрашивается найти периметр другого прямоугольника. Для этого достаточно сложить все найденные стороны:
5 + +8 + 5 + 8 = 26 см.

ОТВЕТ
Площадь другого прямоугольника составляет 40 см.
№3
Площадь квадрата 0,36 см. Найдите его периметр.

Добавлено спустя 1 минутуДима,ответ надо обосновать

Дмитрий Александров:

Найдите площадь поверхности и объём куба, ребро которого равно 6дм.
Во сколько раз уменьшится площадь поверхности и во сколько раз – объём куба,
если его ребро уменьшить вдвое?
Ответ: объём куба=216(дм3),
площадь поверхности=216(дм2),
объём уменьшится в 8 раз, а площадь поверхности в 4 раза.

Наташа Скрипилёва

Посетитель

Сообщений: 16

3696 дней назад

+1

Здравствуйте. Извените, что долго не выходила. Вот мои задачи.
Задача 1: Периметр квадрата увеличили на 40, затем периметр полученного квадрата уменьшили на 40. У какого из квадратов площадь наименьшая?

Решение: Чем больше периметр квадрата, тем больше его площадь. 40 от периметра второго квадрата больше, чем 40 от периметра первого. Значит, наименьший периметр, а тогда и наименьшая площадь у третьего квадрата.

Задача 2
Три наследника разделили квадратный садовый участок со стороной 60 метров на три прямоугольные части равной площади. При этом каждые два наследника стали соседями. Какова общая длина забора, построенного внутри участка для отделения трех частей друг от друга?

Булгакова Елизавета

Посетитель

Сообщений: 21

3696 дней назад

+1

Уберите 6 спичек, не перекладывая остальных, чтобы осталось 5 равных квадратов.

Изображение уменьшено. Щелкните, чтобы увидеть оригинал.

Изображение уменьшено. Щелкните, чтобы увидеть оригинал.

Ответ

Коля Баранов

Посетитель

Сообщений: 15

3724 дня назад

+1

Решите мою задачу. Крест, составленный из 5 квадратов , требуется разрезать на такие части , из которых можно было бы составить 1 квадрат .

Прикрепленные файлы:

zadacha_53707eeeabe8e.docx | 15,35 Кб | Скачали: 539 раз

Александр Федотов

Посетитель

Сообщений: 27

3489 дней назад

+1

Задача: Паркетчик

Паркетчик:

Паркетчик, вырезая квадраты из дерева, проверял их так: он сравнивал длины сторон, и если все четыре стороны были равны, то считал квадрат вырезанным правильно,
Надежна ли такая проверка?

Другой паркетчик:

Другой паркетчик проверял свою работу иначе: он мерил не стороны, а диагонали. Если обе диагонали оказывались равными, паркетчик считал квадрат вырезанным правильно.
а такая надёжна?

Третий паркетчик:

Третий паркетчик при проверке квадратов убеждался в том, что все четыре части, на которые диагонали разделяют друг друга, равны между собой. По его мнению, это доказывало, что вырезанный четырехугольник есть квадрат.
А по-вашему как?

паркетчик:

Такая проверка недостаточна. Четырехугольник мог выдержать это испытание, не будучи вовсе квадратом. Вы видите примеры таких четырехугольников, у которых вед стороны равны, но углы вовсе не прямые (ромбы).

Изображение уменьшено. Щелкните, чтобы увидеть оригинал.

Другой паркетчик:

Эта проверка столь же ненадежна, как и первая. В квадрате, конечно, диагонали равны, но не всякий четырехугольник с равными диагоналями есть квадрат. Это ясно видно из фигур, представленных на рис.

Третий паркетчик:

Проверка могла показать только то, что проверяемый четырехугольник имеет прямые углы, то есть что он прямоугольник. Но равны ли все его стороны, этого проверка не удостоверяла, как видно из рис.

Изображение уменьшено. Щелкните, чтобы увидеть оригинал.

Ответ:

Паркетчикам следовало бы применять к каждому вырезанному четырехугольнику обе проверки сразу, тогда можно быть уверенным, что работа сделана правильно. Всякий ромб, у которого диагонали равны, есть непременно квадрат.

Редактировалось: 2 раза (Последний: 12 мая 2014 в 19:33)

Наталья Леонидовна Будлянская

Посетитель

Сообщений: 174

г.Комсомольск-на-Амуре

3523 дня назад

0

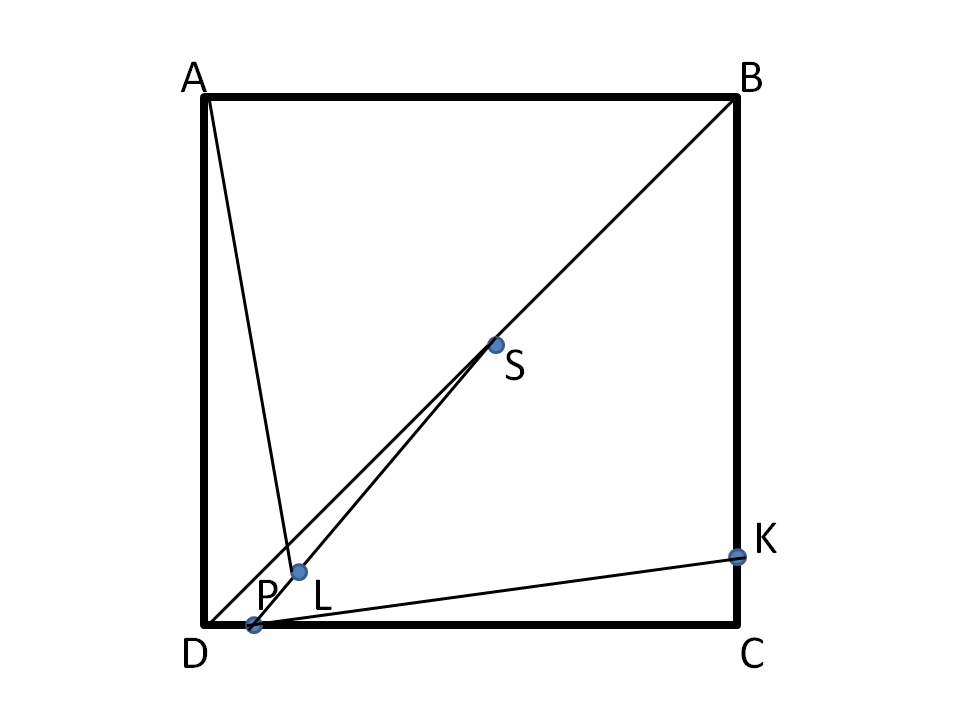
Костя,непонятно,где у тебя А,В,С?

Константин Андоськин:

1) Разделить часть А на 2 равные части. 2) Разделить часть B на 3 ровные части. 3) разделить часть С на 4 ровные части. 4) разделить часть D на 7 ровных частей.

Михаил Сибиряков

Посетитель

Сообщений: 44

Комсомольск-на-Амуре

3686 дней назад

+1

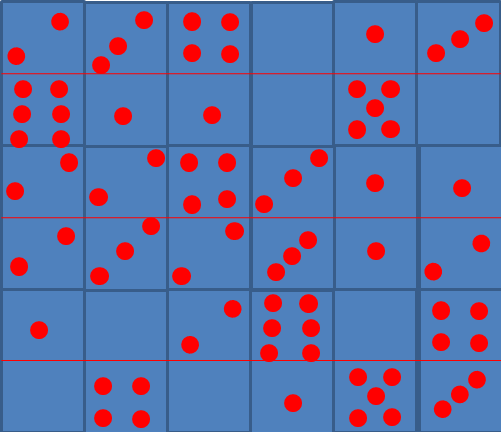
Здравствуйте, я хочу представить вам задачу связанную с домино.
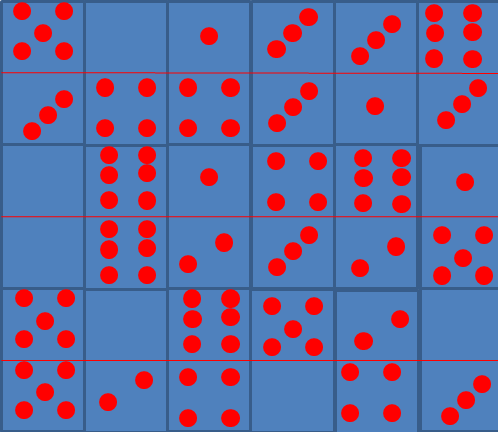
На рис. 1 выложен квадрат из 18 костей домино, в котором сумма очков на каждой вертикали и на больших диагоналях равна 13. Настоящий магический квадрат 6х6.
Задача:составить из 18 костей магический квадрат с суммой очков, также равной 18.
Ответ: один из вариантов рис. 2

Прикрепленные файлы:

1untitled_537092787eeea.png | 17,43 Кб | Скачали: 1291 раз

2untitled_5370927881a04.png | 19,27 Кб | Скачали: 1199 раз

Редактировалось: 2 раза (Последний: 12 мая 2014 в 20:27)

максим лушкин

Посетитель

Сообщений: 4

3874 дня назад

0

В некоторых клетках квадрата 10×10 расставлены несколько крестиков и несколько ноликов. Известно, что нет линии (строки или столбца), полностью заполненной одинаковыми значками (крестиками или ноликами). Однако, если в любую пустую клетку поставить любой значок, то это условие нарушится. Какое минимальное число значков может стоять в таблице?

Павел Постнов

Посетитель

Сообщений: 3

3877 дней назад

+1

Изображение уменьшено. Щелкните, чтобы увидеть оригинал.

софья сидоренко

Посетитель

Сообщений: 6

3877 дней назад

+1

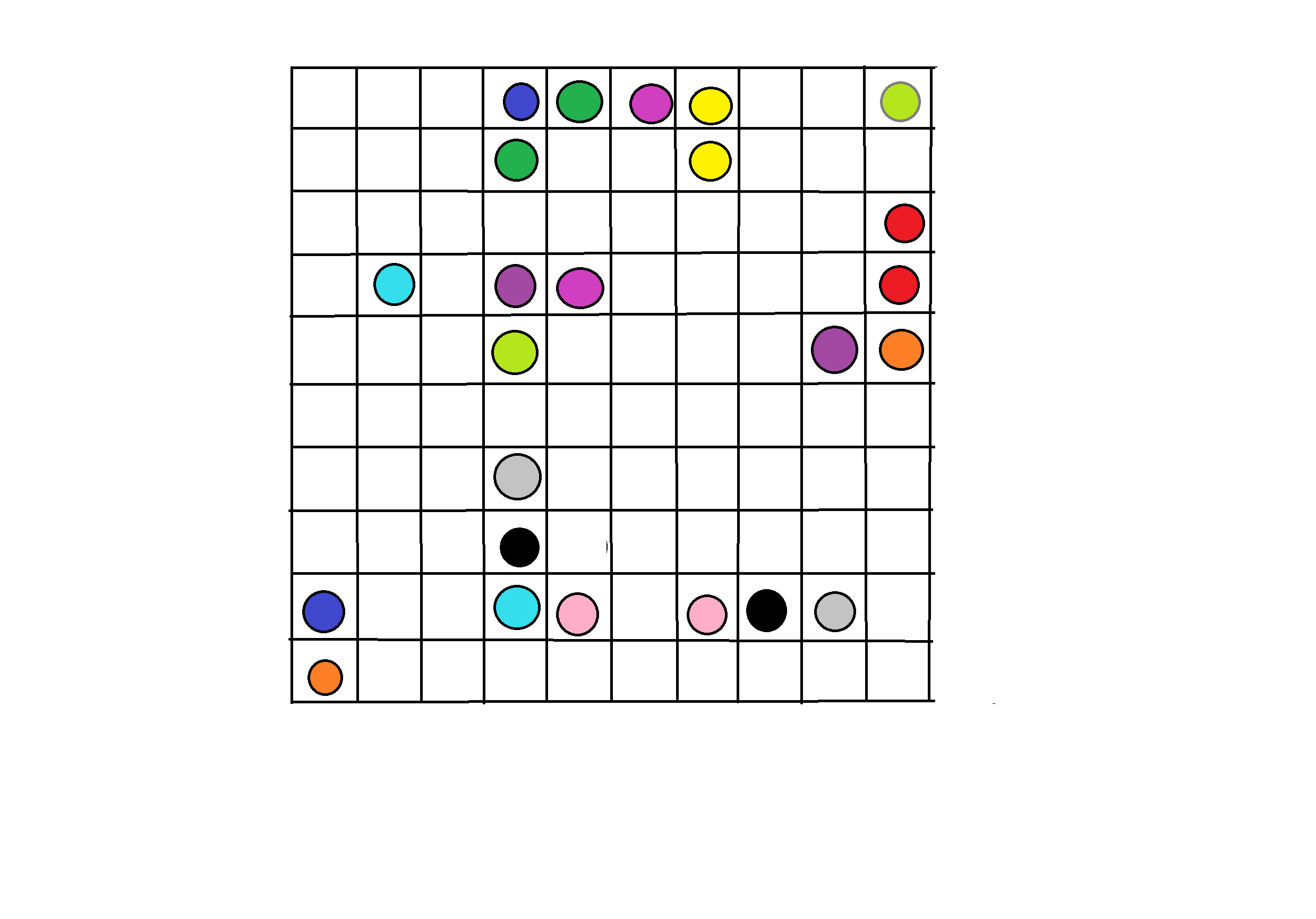
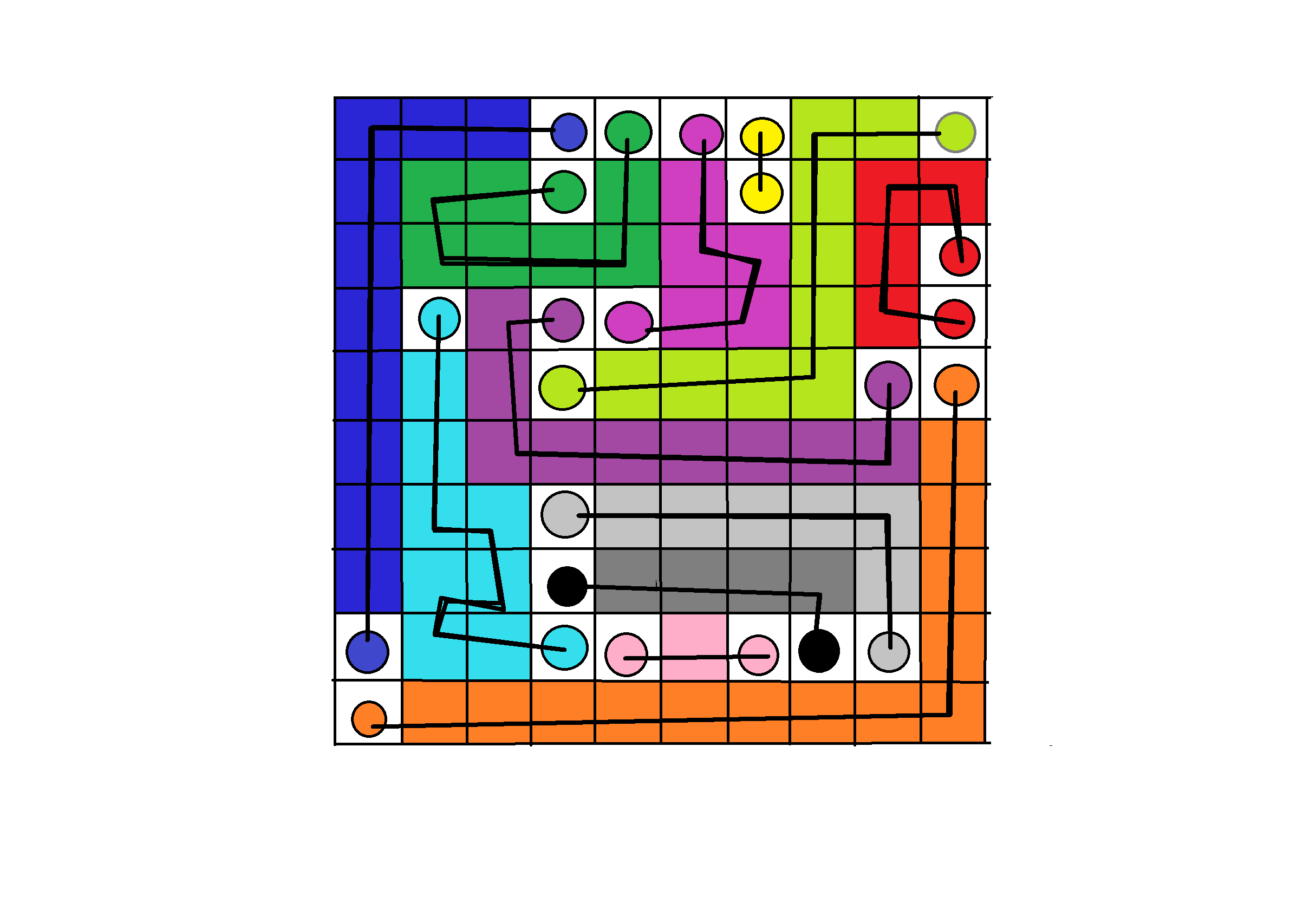
вот задачка!
В квадрате 10*10 расставлены точки, надо соединить точки однго и тогоже цвета так ,чтобы все клетки квадрата были заполнены.

Прикрепленные файлы:

gthkf_5370a1ede67dc.png | 40,03 Кб | Скачали: 1310 раз

trr_5370a1ede7447.png | 129,52 Кб | Скачали: 1250 раз

Влад Гонтарский

Посетитель

Сообщений: 7

3733 дня назад

+1

Передвиньте 2 спички так, чтобы получить 7 квадратов.

Прикрепленные файлы:

novyi-tochechnyi-risunok_5370ab1ad718d.bmp | 612,83 Кб | Скачали: 1217 раз

нелли кириченко

Посетитель

Сообщений: 14

3877 дней назад

0

Задача.
Посчитайте сколько квадратов на расунке?
Ответ : 17 квадратов!!! smile

Прикрепленные файлы:

20140512-222304_5370af8b1b956.jpg | 1544,02 Кб | Скачали: 1248 раз

Наталья Леонидовна Будлянская

Посетитель

Сообщений: 174

г.Комсомольск-на-Амуре

3523 дня назад

+1

Саша,очень хорошая задача. Ты заметил,что она сродни задаче Оксаны Х.о портняжке?

Александр Федотов:

Задача: Паркетчик

Паркетчик:

Паркетчик, вырезая квадраты из дерева, проверял их так: он сравнивал длины сторон, и если все четыре стороны были равны, то считал квадрат вырезанным правильно,
Надежна ли такая проверка?

Другой паркетчик:

Другой паркетчик проверял свою работу иначе: он мерил не стороны, а диагонали. Если обе диагонали оказывались равными, паркетчик считал квадрат вырезанным правильно.
а такая надёжна?

Третий паркетчик:

Третий паркетчик при проверке квадратов убеждался в том, что все четыре части, на которые диагонали разделяют друг друга, равны между собой. По его мнению, это доказывало, что вырезанный четырехугольник есть квадрат.
А по-вашему как?

паркетчик:

Такая проверка недостаточна. Четырехугольник мог выдержать это испытание, не будучи вовсе квадратом. Вы видите примеры таких четырехугольников, у которых вед стороны равны, но углы вовсе не прямые (ромбы).

Изображение уменьшено. Щелкните, чтобы увидеть оригинал.

Другой паркетчик:

Эта проверка столь же ненадежна, как и первая. В квадрате, конечно, диагонали равны, но не всякий четырехугольник с равными диагоналями есть квадрат. Это ясно видно из фигур, представленных на рис.

Третий паркетчик:

Проверка могла показать только то, что проверяемый четырехугольник имеет прямые углы, то есть что он прямоугольник. Но равны ли все его стороны, этого проверка не удостоверяла, как видно из рис.

Изображение уменьшено. Щелкните, чтобы увидеть оригинал.

Ответ:

Паркетчикам следовало бы применять к каждому вырезанному четырехугольнику обе проверки сразу, тогда можно быть уверенным, что работа сделана правильно. Всякий ромб, у которого диагонали равны, есть непременно квадрат.

Добавлено спустя 1 минутуЗамечательно.

софья сидоренко:

вот задачка!
В квадрате 10*10 расставлены точки, надо соединить точки однго и тогоже цвета так ,чтобы все клетки квадрата были заполнены.

Добавлено спустя 3 минутыХорошо.

Влад Гонтарский:

Передвиньте 2 спички так, чтобы получить 7 квадратов.

Добавлено спустя 5 минутНет решения

нелли кириченко:

Задача.
Посчитайте сколько квадратов на расунке?
Ответ : 17 квадратов!!! smile

Добавлено спустя 8 минутНет исходного чертежа.

Павел Постнов:

Изображение уменьшено. Щелкните, чтобы увидеть оригинал.

Добавлено спустя 9 минутОтлично,Миша

Михаил Сибиряков:

Здравствуйте, я хочу представить вам задачу связанную с домино.
На рис. 1 выложен квадрат из 18 костей домино, в котором сумма очков на каждой вертикали и на больших диагоналях равна 13. Настоящий магический квадрат 6х6.
Задача:составить из 18 костей магический квадрат с суммой очков, также равной 18.
Ответ: один из вариантов рис. 2

Юлия Коленченко

Посетитель

Сообщений: 10

3877 дней назад

+1

ВОт моя задача только она не на квадрат а на спички но тоже интересная)))

Имеется две кучки спичек. В первой 7 спичек, во второй - 5. За один ход разрешается взять любое количество спичек, но из одной кучки. Проигрывает тот, кому нечего брать. Кто выигрывает при правильной игре - начинающий или его партнер? И как для этого ему надо играть?

Ответ:

При правильной игре выигрывает начинающий игрок. Его стратегия: первым ходом он должен сравнять количество спичек в кучках, т.е. взять из первой кучки 2 спички. Каждый следующий его ход должен быть "симметричен" ходу второго игрока, т.е. если "второй" берет n спичек из одной кучки, то "первый" должен взять также n спичек, но из другой кучки. Таким образом, если может сделать ход "второй" игрок, то может сделать ход и "первый". Так как после каждого хода количество спичек уменьшается, то наступит момент, когда "второй" не сможет сделать ход (ни в одной из кучек спичек не останется) и проиграет.Добавлено спустя 1 минутуПереложите 4 спички так, чтобы образовалось 10 квадратов.