Лента блогов
Дано n отрезков на прямой. Найти максимальное k, для которого существует точка прямой, покрытая k отрезками («максимальное число слоев»).
Задания для самостоятельной работы (программирование) → 7.2. Участок г-на Чудакова
Участок г-на Чудакова выходит на улицу одной прямолинейной стороной. Г-н Чудаков пожелал отгородить его, но решил, что капитальный забор ему ни к чему, достаточно и отдельных столбиков. Сначала этих столбиков было только два (по краям участка). Потом г-н Чудаков несколько раз убеждался, что такой забор недостаточно надежен, и добавлял к нему новые промежуточные столбики. Найдите самый широкий на данный момент проход в заборе г-на Чудакова.
Входные данные
В первой строке исходного файла записано количество столбиков N (3<=N<=5000). Каждая из следующих N строк содержит координату столбика – целое число, которое по модулю не больше 10^6. Порядок координата в тексте соответствует тому порядку, в котором г-н Чудаков устанавливал столбики.
Выходные данные
В первой строке выходного файла записана ширина искомого прохода, во второй – координаты столбиков, в третьей – номера этих столбиков (по порядку установки столбиков). Первым вывести столбик с меньшей координатой, вторым – с большей.
Пример
Входные данные
В первой строке исходного файла записано количество столбиков N (3<=N<=5000). Каждая из следующих N строк содержит координату столбика – целое число, которое по модулю не больше 10^6. Порядок координата в тексте соответствует тому порядку, в котором г-н Чудаков устанавливал столбики.
Выходные данные
В первой строке выходного файла записана ширина искомого прохода, во второй – координаты столбиков, в третьей – номера этих столбиков (по порядку установки столбиков). Первым вывести столбик с меньшей координатой, вторым – с большей.
Пример
Задания для самостоятельной работы (программирование) → 7.1. Различные числа
Найти количество различных чисел среди элементов данного массива
Задания для самостоятельной работы (программирование) → 6.5. Театральная касса
В одной театральной кассе есть в продаже билеты любой стоимости, выражающейся натуральным числом. При покупке билетов по цене за билет от A до B рублей включительно нужно дополнительно оплатить сервисный сбор в размере C процентов от номинальной стоимости билетов (сервисный сбор не обязательно выражается целым числом рублей, но всегда выражается целым числом копеек). При покупке билетов стоимостью менее A рублей за билет, а также более B рублей за билет, сервисный сбор не берется.
У вас есть X рублей и вам нужно K билетов одинаковой цены (цена обязательно должна выражаться натуральным числом рублей, 0 не считается натуральным). Билеты какого самого дорогого номинала вы можете себе позволить?
Максимальное время работы на одном тесте: 1 секунда
Максимальный объем используемой памяти: 64 мегабайта
Входные данные
Вводятся целые A, B, C, X, K (1 ≤ A ≤ B ≤ 10^9, 0 ≤ C ≤ 1000, 0 ≤ X ≤ 10^9, 1 ≤ K ≤ 100000).
Выходные данные
Если на имеющиеся деньги невозможно приобрести ни одного билета, выведите 0. Иначе выведите натуральное число – номинальную стоимость приобретённых билетов.
Примеры
У вас есть X рублей и вам нужно K билетов одинаковой цены (цена обязательно должна выражаться натуральным числом рублей, 0 не считается натуральным). Билеты какого самого дорогого номинала вы можете себе позволить?
Максимальное время работы на одном тесте: 1 секунда
Максимальный объем используемой памяти: 64 мегабайта
Входные данные
Вводятся целые A, B, C, X, K (1 ≤ A ≤ B ≤ 10^9, 0 ≤ C ≤ 1000, 0 ≤ X ≤ 10^9, 1 ≤ K ≤ 100000).
Выходные данные
Если на имеющиеся деньги невозможно приобрести ни одного билета, выведите 0. Иначе выведите натуральное число – номинальную стоимость приобретённых билетов.
Примеры
Задания для самостоятельной работы (программирование) → 6.4. Черепаха
Домик черепахи расположен в начале прямой узкой грядки, на которой должны прорасти одуванчики – ее любимое лакомство. И вот черепахе приснился вещий сон. Из него она узнала, что наконец-то после полуночи начнут расти одуванчики. Ей даже приснилось, в какой момент времени, и в какой точке грядки вырастет каждый одуванчик. Ровно в полночь черепаха выползла из домика, чтобы съесть все одуванчики и до следующей полуночи вернуться домой.
Черепаха может ползти со скоростью, не превосходящей величины vmax. Одуванчик она съедает, остановившись на время d. Если одуванчик начать есть, но не доесть до конца, то он засыхает, поэтому его надо съедать за один прием. Одуванчики прорастают тем позже, чем дальше они расположены от начала грядки. В одной точке не могут прорастать несколько одуванчиков, а также несколько одуванчиков не могут прорастать в один момент времени.
Требуется определить, в какой момент времени черепаха сможет вернуться домой, съев все одуванчики и затратив на путешествие наименьшее время.
Входные данные
В 1-й строке входного файла находятся 2 целых числа, разделенные пробелом: vmax (в см/мин) и d (в минутах), 0 < vmax ≤ 200, 0 ≤ d ≤ 500.
Во 2-й строке находится число N – количество одуванчиков (в штуках). 0 ≤ N ≤ 1400 при d = 0, в противном случае 0 ≤ N ≤ 200.
В каждой из последующих N строк расположены: целое число xi – расстояние от одуванчика до начала грядки (в сантиметрах), 0 ≤ xi ≤ 32767, и через пробел ti – момент прорастания одуванчика (в формате hh:mm). Пары приведены в порядке возрастания расстояний.
Выходные данные
Выходной файл должен содержать момент времени возвращения черепахи домой (в формате hh:mm), округленный до целых минут в большую сторону.
Примечания
1. В часе – 60 минут, в сутках – 24 часа.
2. Время в сутках изменяется от 00:00 до 23:59.
3. Можете считать, что черепаха не меняет направления движения до тех пор, пока не доползет до последнего одуванчика.
Пример
Черепаха может ползти со скоростью, не превосходящей величины vmax. Одуванчик она съедает, остановившись на время d. Если одуванчик начать есть, но не доесть до конца, то он засыхает, поэтому его надо съедать за один прием. Одуванчики прорастают тем позже, чем дальше они расположены от начала грядки. В одной точке не могут прорастать несколько одуванчиков, а также несколько одуванчиков не могут прорастать в один момент времени.
Требуется определить, в какой момент времени черепаха сможет вернуться домой, съев все одуванчики и затратив на путешествие наименьшее время.
Входные данные
В 1-й строке входного файла находятся 2 целых числа, разделенные пробелом: vmax (в см/мин) и d (в минутах), 0 < vmax ≤ 200, 0 ≤ d ≤ 500.
Во 2-й строке находится число N – количество одуванчиков (в штуках). 0 ≤ N ≤ 1400 при d = 0, в противном случае 0 ≤ N ≤ 200.
В каждой из последующих N строк расположены: целое число xi – расстояние от одуванчика до начала грядки (в сантиметрах), 0 ≤ xi ≤ 32767, и через пробел ti – момент прорастания одуванчика (в формате hh:mm). Пары приведены в порядке возрастания расстояний.
Выходные данные
Выходной файл должен содержать момент времени возвращения черепахи домой (в формате hh:mm), округленный до целых минут в большую сторону.
Примечания
1. В часе – 60 минут, в сутках – 24 часа.
2. Время в сутках изменяется от 00:00 до 23:59.
3. Можете считать, что черепаха не меняет направления движения до тех пор, пока не доползет до последнего одуванчика.
Пример
Задания для самостоятельной работы (программирование) → 6.3. Коровы и стойла
На прямой расположены стойла, в которые необходимо расставить коров так, чтобы минимальное расстояние между коровами было как можно больше.
Входные данные
В первой строке вводятся числа N (2 < N < 10001) – количество стойл и K (1 < K < N ) – количество коров. Во второй строке задаются N натуральных чисел в порядке возрастания – координаты стойл (координаты не превосходят 10^9).
Выходные данные
Выведите одно число – наибольшее возможное допустимое расстояние.
Пример
Входные данные
В первой строке вводятся числа N (2 < N < 10001) – количество стойл и K (1 < K < N ) – количество коров. Во второй строке задаются N натуральных чисел в порядке возрастания – координаты стойл (координаты не превосходят 10^9).
Выходные данные
Выведите одно число – наибольшее возможное допустимое расстояние.
Пример
Задания для самостоятельной работы (программирование) → 6.2. Два массива-2
Дано два массива. Для каждого элемента второго массива определите, сколько раз он встречается в первом массиве.
Ограничение по времени: 1 секунда
Ограничение по памяти: 64 мегабайта
Входные данные
Первая строка входных данных содержит одно число N (1 ≤ N ≤ 10^5) – количество элементов в первом массиве. Далее идет N целых чисел, не превосходящих по модулю 10^9 – элементы первого массива, Далее идет количество элементов M во втором массиве и M элементов второго массива с такими же ограничениями.
Выходные данные
Выведите M чисел: для каждого элемента второго массива выведите, сколько раз такое значение встречается в первом массиве.
Пример
Ограничение по времени: 1 секунда
Ограничение по памяти: 64 мегабайта
Входные данные
Первая строка входных данных содержит одно число N (1 ≤ N ≤ 10^5) – количество элементов в первом массиве. Далее идет N целых чисел, не превосходящих по модулю 10^9 – элементы первого массива, Далее идет количество элементов M во втором массиве и M элементов второго массива с такими же ограничениями.
Выходные данные
Выведите M чисел: для каждого элемента второго массива выведите, сколько раз такое значение встречается в первом массиве.
Пример
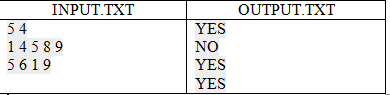
Задания для самостоятельной работы (программирование) → 6.1. Два массива-1
Входные данные
В первой строке входных данных содержатся натуральные числа N и K (0 < N ,K <= 100000 ). Во второй строке задаются N элементов первого массива, отсортированного по возрастанию, а в третьей строке – K элементов второго массива. Элементы обоих массивов - целые числа, каждое из которых по модулю не превосходит 10^9.
Выходные данные
Требуется для каждого из K чисел вывести в отдельную строку "YES", если это число встречается в первом массиве, и "NO" в противном случае.
Пример
В первой строке входных данных содержатся натуральные числа N и K (0 < N ,K <= 100000 ). Во второй строке задаются N элементов первого массива, отсортированного по возрастанию, а в третьей строке – K элементов второго массива. Элементы обоих массивов - целые числа, каждое из которых по модулю не превосходит 10^9.
Выходные данные
Требуется для каждого из K чисел вывести в отдельную строку "YES", если это число встречается в первом массиве, и "NO" в противном случае.
Пример
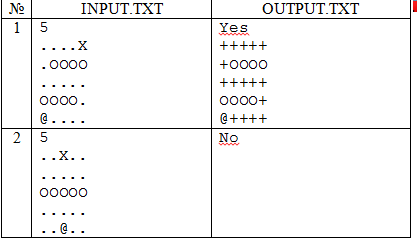
Задания для самостоятельной работы (программирование) → 5.5. Шарики
В таблице из N строк и N столбцов некоторые клетки заняты шариками, другие свободны. Выбран шарик, который нужно переместить, и место, куда его нужно переместить. Выбранный шарик за один шаг перемещается в соседнюю по горизонтали или вертикали свободную клетку. Требуется выяснить, возможно ли переместить шарик из начальной клетки в заданную, и, если возможно, то найти путь из наименьшего количества шагов.
Входные данные
В первой строке входного файла INPUT.TXT находится число N, в следующих N строках - по N символов. Символом точки обозначена свободная клетка, латинской заглавной O - шарик, @ - исходное положение шарика, который должен двигаться, латинской заглавной X - конечное положение шарика. (2 <= N <= 50)
Выходные данные
В выходной файл OUTPUT.TXT выведите в первой строке Yes, если движение возможно, или No, если нет. Если движение возможно, то далее следует вывести N строк по N символов - как и на вводе, но букву X, а также все точки по пути следует заменить плюсами. Если решений несколько, выведите любое.
Примеры
Входные данные
В первой строке входного файла INPUT.TXT находится число N, в следующих N строках - по N символов. Символом точки обозначена свободная клетка, латинской заглавной O - шарик, @ - исходное положение шарика, который должен двигаться, латинской заглавной X - конечное положение шарика. (2 <= N <= 50)
Выходные данные
В выходной файл OUTPUT.TXT выведите в первой строке Yes, если движение возможно, или No, если нет. Если движение возможно, то далее следует вывести N строк по N символов - как и на вводе, но букву X, а также все точки по пути следует заменить плюсами. Если решений несколько, выведите любое.
Примеры
Задания для самостоятельной работы (программирование) → 5.4. Вершины двоичного дерева
Написать программу, которая печатает (по одному разу) все вершины двоичного дерева
 Центр поддержки одаренных детей ХКИРО
Центр поддержки одаренных детей ХКИРО