Центр поддержки одаренных детей ХКИРО

Предлагаю свою задачу Виды прямо и справа совпадают,а сверху иной(см.рис)
Сколько кубиков минимально убраны?

Павел, ты забыл сформулировать задачу!Добавлено спустя 2 минутыСаша, отличная задача, надеюсь ,будет и решение ?

Ренат,сформулируй задачу и предоставь,пожалуйста, свой ответ

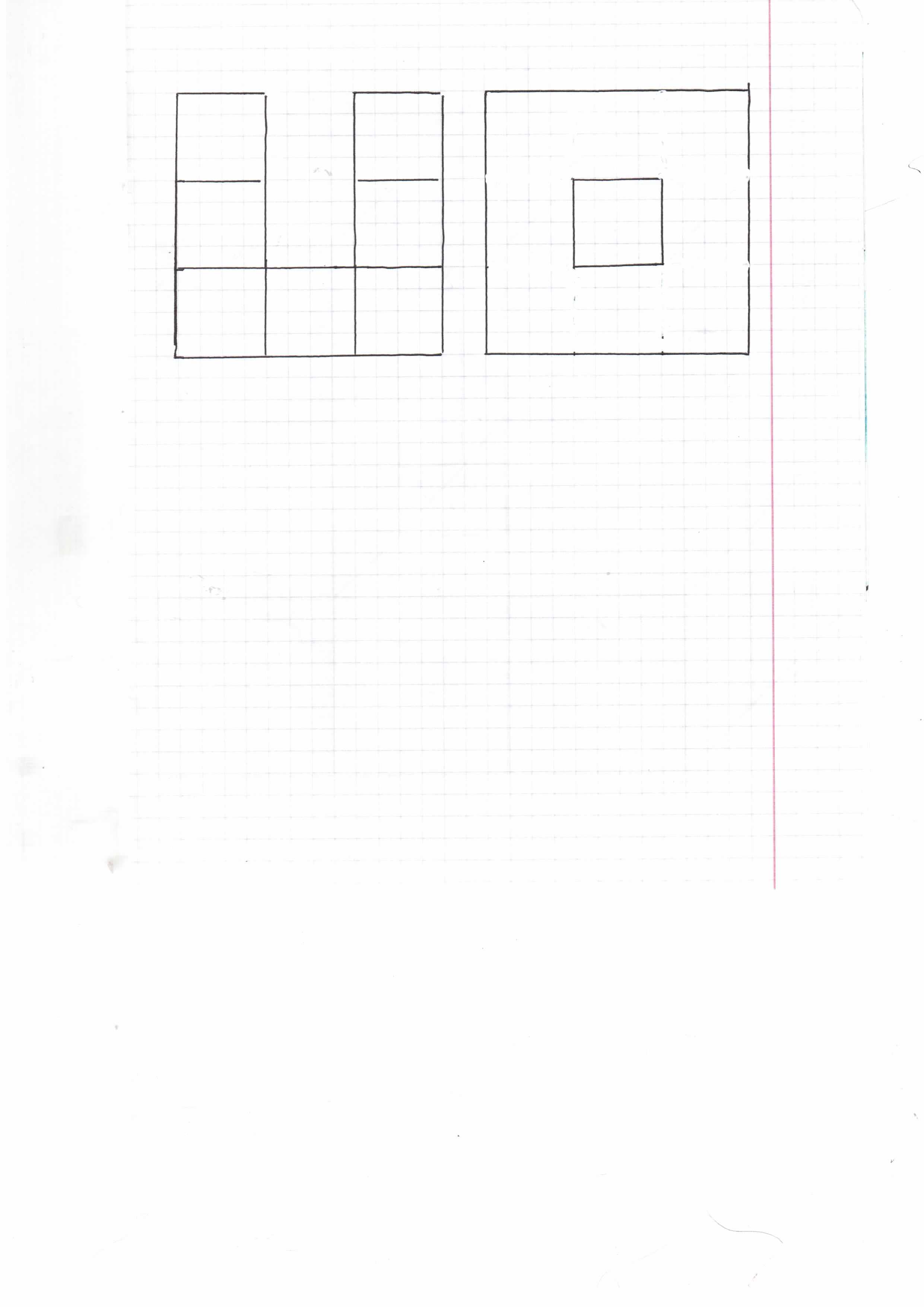
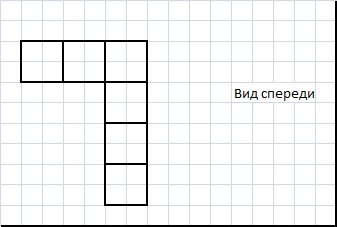
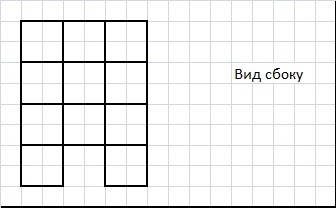
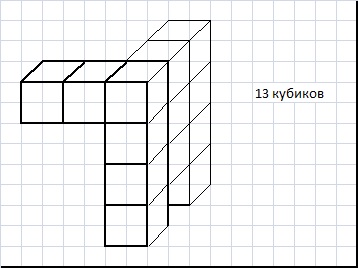
Куб 5х5х5 сделан из 125 кубиков. Какое наименьшее количество кубиков нужно вынуть, чтобы вид спереди, сверху и справа был таким, как на рисунке?

Ответ: 13

Куб 3х3х3 сделан из 27 кубиков. Какое наименьшее и наибольшее количество кубиков нужно вынуть, чтобы вид спереди и сверху были такими, как на рисунке?

Решение: 1)3+2=5(куб.)
2)1+6+7=14(куб.)
Ответ: 5 куб.-наименьшее количество ; 14 куб.-наибольшее количество.

Куб 3х3х3 сделан из 27 кубиков. Какое наибольшее количество кубиков нужно вынуть, чтобы вид спереди и с верху был таким,как на рисунке?
вид спереди:

вид сверху:

Размеры моего параллелепипеда 4x5[x5. Даны вид сбоку и вид сверху. Какое минимальное количество кубиков нужно убрать?

Ответ к моей задаче:
Убрано 3 ряда кубиков по 5 кубиков в каждом ряду.

3 х 5= 15 кубиков
Соответственно, нужно убрать 15 кубиков.

Алиса,ты представила правильную задачу и решение,если добавить в вопросе слово "минимальное". фрося ,Аня,Ульяна,предоставьте свои ответы и, желательно ,решения.
Ребята,участвующие в олимпиаде "Золотой ключик",ваши работы проверены. Привожу результаты:
1Федотов-102 б
2,Михалев-102 б
3Маслоовская-96
4.Казелько-96
5.Бабина-90
6.Бржезицкий-87
?.Баранов-87 Молодцы,отличные результаты! Ждем дипломы.

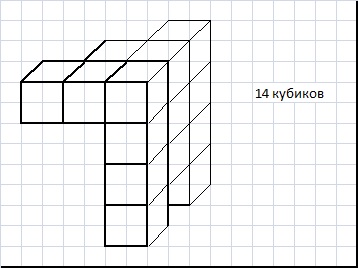
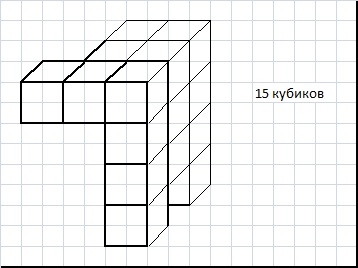
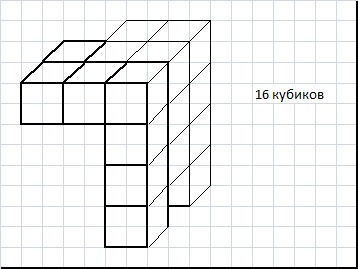
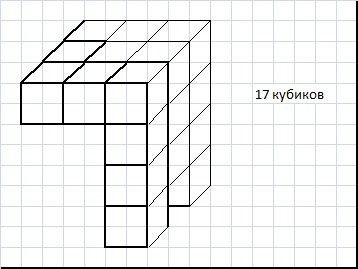
Я составил фигуры из кубиков. Даны вид спереди и вид сбоку. По сколько кубиков можно составить фигуры?

Ответы:13, 14, 15, 16 и 17 кубиков

Здравствуйте я помогаю выложить задачу Яны.
Дан вид сверху и сбоку.
Сколько надо убрать, чтобы получить куб с такими видами

сделайте куб чтобы он выглядил спереди и с боку так как на картинке.

Сколько кубов надо убрать из куба 5x5x5, чтобы вид спереди, сверху и сбоку был таким, как на картинке.

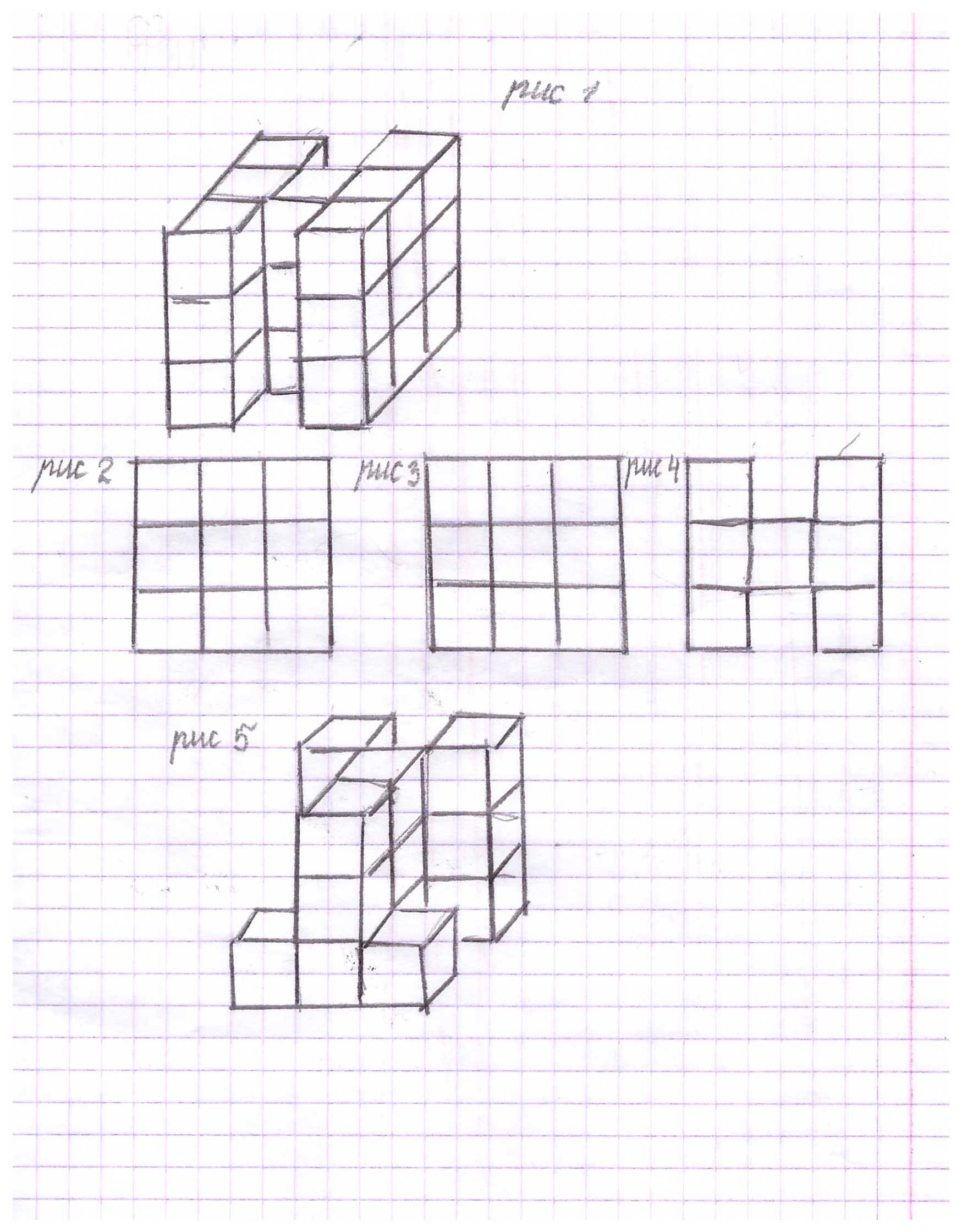
Дана фигура, изображенная на рис. 1. Ее вид спереди, сбоку и сверху - на рис. 2, 3, 4 соответственно. Какое максимальное количество кубиков можно убрать, чтобы ее вид со всех сторон не изменился.
ответ: 6 кубиков (рис.5)
предложите свои варианты.