Центр поддержки одаренных детей ХКИРО

Даны три столбика: A, B и C. На столбике A находятся N дисков разного диаметра, пронумерованные сверху вниз. Причем они расположены так, что каждый меньший диск находится на большем. Требуется переместить эти диски на диск C, сохранив их взаиморасположение. Столбик B разрешается использовать как вспомогательный. При решении за один шаг допускается перемещать только один из верхних дисков какого-либо столбика. Кроме того, больший диск никогда не разрешается класть на диск меньшего диаметра.

Реализовать алгоритм Евклида с помощью рекурсивной функции

По заданному натуральному числу А требуется найти наибольшее число В такое, что B^2 <= A.

Время: 1 сек. Память: 16 Мб

Входные данные
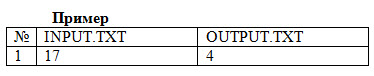
Во входном файле INPUT.TXT записано натуральное число A (A <= 10^3000).

Выходные данные
В выходной файл OUTPUT.TXT выведите максимальное натуральное число B, квадрат которого не превосходит A. Число B следует выводить без лидирующих нулей.

Перевести длинное целое в системы счисления с основаниями 2, 8, 16.

Для натуральных чисел A и B требуется вычислить значение A^B.

Время: 1 сек. Память: 16 Мб

Входные данные
Входной файл INPUT.TXT в первой строке содержит числа A и B, разделенные пробелом. (1 <= A <= 9, 1 <= B <= 10^4)

Выходные данные
В выходной файл OUTPUT.TXT выведите одно число – результат возведения в степень, без лидирующих нулей.

Даны целые неотрицательные числа M и N. Требуется найти произведение этих чисел.

Время: 1 сек. Память: 16 Мб

Входные данные
Входной файл INPUT.TXT содержит в первой строке число M, а во второй строке – число N. (0 <= M, N <= 10^2500)

Выходные данные
В выходной файл OUTPUT.TXT выведите произведение чисел M и N.

Создать и отладить модуль с разобранными на лекции алгоритмами: сравнение, сложение, вычитание длинных целых, ввод-вывод длинных целых, умножение длинного целого на короткое, умножение длинных целых, деление длинных целых.

Напомним, что палиндромом называется строка, одинаково читающаяся с обеих сторон. Например, строка «ABBA» является палиндромом, а строка «ABC» - нет. Необходимо определить, в каких системах счисления с основанием от 2 до 36 представление заданного числа N является палиндромом.
В системах счисления с основанием большим 10 в качестве цифр используются буквы латинского алфавита: A, B, ... , Z.

Время: 1 сек. Память: 16 Мб

Входные данные
Входной файл INPUT.TXT содержит заданное число N в десятичной системе счисления (1 <= N <= 109).

Выходные данные
Если соответствующее основание системы счисления определяется единственным образом, то выведите в первой строке выходного файла OUTPUT.TXT слово «unique», если оно не единственно — выведите в первой строке выходного файла слово «multiple». Если же такого основания системы счисления не существует — выведите в первой строке выходного файла слово «none».
В случае существования хотя бы одного требуемого основания системы счисления выведите через пробел в возрастающем порядке во второй строке выходного файла все основания системы счисления, удовлетворяющие требованиям.

Имеется N банок с целочисленными объемами V1, V2, …, Vn литров, пустой сосуд и кран с водой. Можно ли с помощью этих банок налить в сосуд ровно V литров воды?

Необходимо вывести все простые числа от M до N включительно

Время: 1 сек. Память: 16 Мб

Входные данные
Входной файл INPUT.TXT содержит два натуральных числа M и N, разделенных пробелом (2 <= M <= N <= 106)

Выходные данные
В выходной файл OUTPUT.TXT выведите в одной строке через пробел все простые числа от M до N в порядке возрастания. Если таковых чисел нет, то следует вывести «Absent».