Центр поддержки одаренных детей ХКИРО

В таблице из N строк и N столбцов некоторые клетки заняты шариками, другие свободны. Выбран шарик, который нужно переместить, и место, куда его нужно переместить. Выбранный шарик за один шаг перемещается в соседнюю по горизонтали или вертикали свободную клетку. Требуется выяснить, возможно ли переместить шарик из начальной клетки в заданную, и, если возможно, то найти путь из наименьшего количества шагов.

Входные данные
В первой строке входного файла INPUT.TXT находится число N, в следующих N строках - по N символов. Символом точки обозначена свободная клетка, латинской заглавной O - шарик, @ - исходное положение шарика, который должен двигаться, латинской заглавной X - конечное положение шарика. (2 <= N <= 50)

Выходные данные
В выходной файл OUTPUT.TXT выведите в первой строке Yes, если движение возможно, или No, если нет. Если движение возможно, то далее следует вывести N строк по N символов - как и на вводе, но букву X, а также все точки по пути следует заменить плюсами. Если решений несколько, выведите любое.

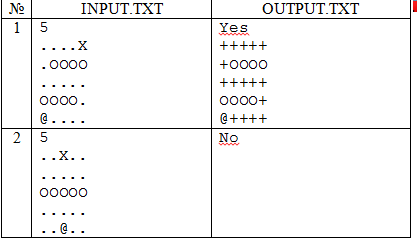
Примеры

Написать программу, которая печатает (по одному разу) все вершины двоичного дерева

Написать программу подсчета числа листьев в двоичном дереве.

Даны три столбика: A, B и C. На столбике A находятся N дисков разного диаметра, пронумерованные сверху вниз. Причем они расположены так, что каждый меньший диск находится на большем. Требуется переместить эти диски на диск C, сохранив их взаиморасположение. Столбик B разрешается использовать как вспомогательный. При решении за один шаг допускается перемещать только один из верхних дисков какого-либо столбика. Кроме того, больший диск никогда не разрешается класть на диск меньшего диаметра.

Реализовать алгоритм Евклида с помощью рекурсивной функции