Центр поддержки одаренных детей ХКИРО

Вот моя сказка:
В королевстве чисел было много государств.В одном из государств жили цифры 1,2,3,4,5,6,7,8,9 и 0.Однажды они стали спорить о том, какая же цифра самая полезная и нужная. .Долго спорили цифры. Вот наконец решили они пойти к числу 10 за помощью.Число 10 - мудрое число, оно всегда могло разрешить любой спор. "Я считаю, что каждый из вас очень нужный и полезный, ведь если бы не было определенной цифры , то и не было бы определенного числа. Например, как я: я состою из цифр 1 и 0. Так и другие числа не могут обходиться без каждого из вас". Теперь цифры поняли, как каждый из них важен и больше не ссорились.Добавлено спустя 4 минутыА вот стихотворение о числах С. Я. Маршака
Не из учебника задача,
Вот один иль единица,
Очень тонкая как спица.
А вот это цифра два.
Полюбуйся, какова
Выгибает двойка шею,
Волочится хвост за нею.
А за двойкой - посмотри -
Выступает цифра три.
Тройка третий из значков. -
Состоит из 2х крючков.
За тремя идет четыре
Острый локоть оттопыря.
А потом пошла плясать
По бумаге цифра пять.
Руку влево протянула,
Ножку круто изогнула.
Цифра шесть - дверной замочек:
Сверху крюк, внизу кружочек.
Вот семерка - кочерга,
У нее одна нога.
У восьмерки два кольца
Без начала и конца.
Цифра девять иль девятка, -
Цифровая акробатка:
Если на голову встает,
Цифрой шесть девятка станет.
Цифра вроде буквы О
Это ноль, иль ничего:
Круглый ноль такой хорошенький,
Но не знает ничегошеньки!
Если ж слева, рядом с ним,
Единицу поместим,
Он побольше станет весить,
Потому что это - десять.

Здравствуйте.На уроке у Сергея Владимировича мне запомнился факт о делении чисел: возьмем,например число 25-это квадрат 5, количество делителей у него 3; число 4-это квадрат 2, количество делителей 3; число 49-квадрат 7, количество его делителей 3.Можно сделать вывод: количество делителей будет нечётным у чисел квадратов.

Здравствуйте.Я нашла числа,у которых есть такое же свойство,как и у 132,:135,124,168,216,264,312,324,612,648,735,864,936, 111,222,333,444...
Такие числа я назвала бы кратновходящими.

Здравствуйте.Я расскажу на какие подмножества можно разложить множество натуральных чисел.
Множества натуральных чисел можно разложить на следующие подмножества:
1)Числа, являющиеся квадратом натурального числа и числа,не являющиеся квадратом числа.(Чтобы найти квадрат числа, нужно число умножить на само себя.) Например,в раздел с числами, являющимися квадратом я отнесу числа: 4,9,16,25,36,49,64,81 и др. А в раздел с числами,не являющимися квадратом я отнесу остальные числа.
2)Числа, являющиеся кубом натурального числа и числа, не являющиеся кубом числа.(Чтобы найти куб числа, нужно число перемножить на само себя 3 раза)Например,в раздел с числами, являющимися кубом я отнесу числа: 27,64,125,216,343,512,729 и др.А в раздел с числами, не являющимися кубом я, соответственно отнесу остальные натуральные числа.

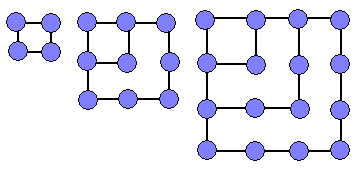
Здравствуйте!Я расскажу о треугольных и квадратных числах.
Треугольные и квадратные числа являются одним из разделов фигурных чисел.
Треугольное число - это число кружков, которые могут быть расставлены в форме правильного треугольника. Последовательность треугольных чисел:1,3,6,10,15,21,28,38,45,55...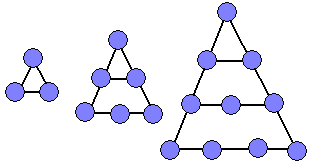

Квадратное число - это число, являющееся квадратом некоторого целого числа. Например, 9-это квадратное число, так как, оно может быть представлено в виде произведения 3х3(может быть представлено в виде квадрата 3х3 точки)
Последовательность квадратных чисел:1,4,9,16,25,36,49,64,81,100...

Здравствуйте!Я нашла ещё одну задачу по теме "Квадрат".
Звездочки и крестики. Для решения этой головоломки требуется определенная изобретательность, так как подвох заключается в угловом расположении одного из крестиков.
Головоломка заключается в том, чтобы разрезать данный квадрат вдоль линий на 4 части так, чтобы все части были одинакового размера и одной формы и чтобы каждая из частей содержала по звездочке и по крестику.

Решение:1)6х6=36(кв.клет.)-площадь квадрата.
2)36:4=9(кл.)-столько клеток должно быть в каждой части.
Ответ:

Моя задача на тему "Площади".
У одного фермера был квадратный участок земли, на котором росли 24 дерева. В своем завещании он пожелал, чтобы каждый из его восьми сыновей получил одинаковое количество земли и равное число деревьев.
Как наипростейшим образом разделить землю?

Решение: Каждому сыну должен достаться участок с 3 деревьями, т.к. 24:8=3(д.)
Ответ:

Задача:
Рассматривая каркас куба сначала спереди (вид А), затем слева (вид В) и, наконец, сверху (вид С), прочитайте слово, образованное жирными линиями.

Ответ:1)-бор 2)-ель 3)-бес

Куб 3х3х3 составлен из 14 белых и 13 чёрных кубиков со стороной 1 ед. Столбик-это три кубика, стоящие вдоль одного направления:длины, ширины или высоты. Может ли быть так, что в каждом столбике нечётное количество белых кубиков?
Решение: нет.Если в каждом из 9 вертикальных столбиков было бы нечётное число белых кубиков, то и всего их было бы нечётное число.

Здравствуйте.Я нашла интересную задачу про куб.
1)Для того, чтобы покрасить кубик, изображённый на левом рисунке, потребуется 9 кг краски.Сколько краски потребуется, чтобы покрасить фигуру, изображённую на правом рисунке?

Решение:S пов. 1 фигуры=9х6=54
S пов. 2 фигуры=9х3+5х3+12=54
Ответ: так как площади равны, то краски понадобится столько же, т.е. 9 кг