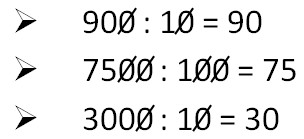Центр поддержки одаренных детей ХКИРО

Наталья Леонидовна, я написала заключение, но думаю, надо его доработать. Вот заключение:

Изучив подробно тему «Квадрат», я достигла своих целей :
Я узнала свойства квадрата
Научилась решать задачи на тему «Квадрат»
Ознакомилась с признаками квадрата
Показала разнообразие применения квадрата через решения различных задач
И конечно, я достигла своей главной цели- я показала, насколько удивительна такая простая фигура-квадрат

Здравствуте, вот моя сказка на тему "Мир чисел"
Однажды в селе Чисел шла цифра 2. Навстречу к цифре 2 идет цифра 5. Цифра 2 говорит:
А ты знаешь, что я могу поделиться на любое четное число?
Знала. Но зато я могу поделится на числа, которые оканчиваются на 5 и 0.
Что то ты попутала. Разве можно поделить 0 на 5?
Я немного ошиблась. И все таки математика без меня- как человек без ног!
Нет, это математика без меня- как человек без рук.
Нет!
Да!
Тут подходит цифра 3.
Что происходит?
Цифра 5 говорит, что математика без нее- как человек без рук!
-Не правда! Я такого не говорила! Это цифра 2 тут хвасталась!
-Успокойтесь! Математике нужны все числа!!!
И правда! Но все таки я лучше! – сказала цифра 5
Нет я!
Мы все нужны математике! И не будьте такими самолюбивыми!!!

Наталья Леонидовна, я сделала до конца работу.Посмотрите , у меня в виде презентации и документа

Наталья Леонидовна, я сделала до конца работу.Посмотрите , у меня в виде презентации и документа
При́знак дели́мости — алгоритм, позволяющий сравнительно быстро определить, является ли число кратным заранее заданному[1]. Если признак делимости позволяет выяснить не только делимость числа на заранее заданное, но и остаток от деления, то его называют признаком равноостаточности.

Признак делимости на 10, 100 и 1000
На 10 делятся нацело только те числа, последняя цифра которых нуль.
На 100 делятся нацело только те числа, две последние цифры которых нули.
На 1000 делятся нацело только те числа, три последние цифры нули.
Чтобы было проще делить на 10, 100 и 1000, просто зачеркивайте одинаковое количество нулей в обоих числах.
Примеры:Добавлено спустя 14 минутПризнак делимости на 11
Число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11.

В самом деле признак делимости на 11 очень интересен, попробуем разобраться на примере:
Проверим, делится ли 671 на 11 .

Итак, цифры которые стоят на нечетных местах - это 6 (стоит на первом месте) и 1 (стоит на третьим месте). Цифра, которая стоит на четном месте это 7 (стоит на втором месте). 6 + 1 = 7. Сумма цифр стоящих на нечетном месте равна сумме цифр на четном месте, значит 671 делится на 11.

Проверим делится ли 3905 на 11
Цифры которые стоят на нечетных местах - это 3 (стоит на первом месте) и 0 (стоит на третьим месте). Цифры, которые стоят на четном месте это 9 (стоит на втором месте) и 5 (стоит на четвертом месте).

3 + 0 ≠ 9 + 5 → 3 ≠ 14 Сумма цифр, стоящих на нечетном месте, не равна сумме цифр на четном месте, но суммы цифр отличаются ровно на 11. 14 - 3 = 11. Значит 3905 делится на 11.

Женщина несла на базар корзину яиц.
Прохожий нечаянно толкнул женщину, корзина упала и яйца разбились.
Виновник несчастья, желая возместить потерю, поинтересовался, сколько яиц было в корзине.
- Точно не помню, ответила женщина, - но знаю, что когда я вынимала из корзины по 2, по 3, по 4, по 5, по 6 яиц, в корзине оставалось одно яйцо, а когда я вынимала по 7, в корзине ничего не оставалось.

Сколько яиц было в корзине ?

Женщина несла на базар корзину яиц.
Прохожий нечаянно толкнул женщину, корзина упала и яйца разбились.
Виновник несчастья, желая возместить потерю, поинтересовался, сколько яиц было в корзине.
- Точно не помню, ответила женщина, - но знаю, что когда я вынимала из корзины по 2, по 3, по 4, по 5, по 6 яиц, в корзине оставалось одно яйцо, а когда я вынимала по 7, в корзине ничего не оставалось.

Сколько яиц было в корзине ?
Если бы из корзины вынули одно яйцо, оставшееся количество яиц делилось бы нацело на 2, 3, 4, 5, и 6.
Числа, для которых это выполняется, - это 60 и числа, кратные 60-ти.
Задача сводится к нахождению числа, кратного 60-ти, которое делилось бы на 7 после добавления 1 ( или, иными словами, при делении на 7 давало бы остаток 6).

Число 60 при делении на 7 дает остаток 4. Следовательно, нужно найти число, кратное 4-ем, которое было бы на 6 больше числа, кратного 7-ми.

Это число - остаток от деления общего числа яиц на 7, оно равно
7· 2 +6 = 20. **

В этом числе остаток 4 содержится пятикратно, значит, первоначально в корзине было 60 · 5 + 1 = 301 яйцо.

** Замечание. Следующее, большее число, обладающее указанным свойством, равно 7 · 6 + 6 = 48.

Такой остаток может быть получен при 12-кратном повторении порции 60 яиц (48 : 4 = 12).

В этом случае, число яиц в корзине составило бы 60 · 12 + 1 = 721 яйцо - вариант, в рассматриваемой ситуации нереальный. Такую корзину женщине не поднять.
ОТВЕТЬ НА ВОПРОСЫ:

Признак делимости на 7

1.У данного числа найдем сумму цифр, стоящих на четных местах, и сумму цифр, стоящих на нечетных местах. Если эти суммы равны или их разность делится на 7, то и само число делится на 7
2. Число делится на 7, когда две его последние цифры делятся на 7
3. Число делится на 7 тогда и только тогда, когда разность между числом без последних трех его цифр и числом, образованным последними его тремя цифрами делится на 7

Признак делимости на 8

1.Число делится на 8, когда число, образованное тремя его последнии цифрами делится на 8.
2. Число делится на 8, когда две его последние цифры делятся на 8
3. Число делится на 8 тогда и только тогда, когда разность между числом без последних трех его цифр и числом, образованным последними его тремя цифрами делится на 8

Наталья Леонидовна, я выставила наброски своей исследовательской работы. Посмотрите.

Задача 1
Доказать, что n3+3n2+5n+3 делится на 3 при любом натуральном n.

Решение:
представим наш многочлен в виде суммы двух слагаемых:
n3+3n2+5n+3=n3+3n2+2n+3n+3=n(n2+3n+2)+3(n+1)=n(n+1)(n+2)++3(n+1), первое слагаемое есть произведение трех последовательных натуральных чисел, одно из которых обязательно делится на 3, а второе слагаемое содержит множитель 3, => оно делится на 3, а значит и вся сумма делится на 3.



Задача 2
Какой остаток при делении на 5 дает число 33333?

Решение:
33333=33332+1 – число оканчивается цифрой 3, остаток от деления на 5 есть 3.



Я нашла презентацию про Делимость чисел. Заходите в мой кабинет, посмотрите.

Ребята, заходите в мой личный кабинет! Я выставила презентацию про свойства натуральных чисел.

Какие свойства у натуральных чисел?
В конце XIX века итальянским математиком Д. Пеано были сформулированы свойства следования натуральных чисел:

1 — это первое натуральное число, перед ним нет других натуральных чисел. То есть единица не следует ни за каким другим натуральным числом.
За каждым натуральным числом следует другое натуральное число. Причем только одно. Из этого следует, что каждое натуральное число, кроме 1, следует за другим.
Подмножество натуральных чисел, начинающееся с 1, после которой друг за другом следуют натуральные числа, содержит все натуральные числа.

Подмно́жество в теории множеств — это понятие части множества.
На диаграмме кругов Эйлера видно, что A является подмножеством B, а B является надмножеством A.



Числа, делящиеся на 9.
9 групп чисел вида 9n; 9n+1; 9n+2; 9n+3; 9n+4; 9n+5; 9n+6; 9n+7; 9n+8.
где n- натурально